
如图①所示,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
⑴试说明:OB∥AC;
⑵如图②,若点E、F在BC上,且∠FOC=∠AOC ,OE平分∠BOF.试求∠EOC的度数;
⑶在⑵的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
⑷在⑶的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.

(1)理由见解析;(2)40°;(3)不变,1:2;(4)60.
【解析】
试题分析:(1)由同旁内角互补,两直线平行证明.
(2)由∠FOC=∠AOC,并且OE平分∠BOF得到∠EOC=∠EOF+∠FOC= (∠BOF+∠FOA)=
(∠BOF+∠FOA)= ∠BOA,算出结果.
∠BOA,算出结果.
(3)先得出结论:∠OCB:∠OFB的值不发生变化,理由为:由BC与AO平行,得到一对内错角相等,由∠FOC=∠AOC,等量代换得到一对角相等,再利用外角性质等量代换即可得证;
(4)由(2)(3)的结论可得.
(1)∵BC∥OA,
∴∠B+∠O=180°,又∵∠B=∠A,
∴∠A+∠O=180°,
∴OB∥AC;
(2)∵∠B+∠BOA=180°,∠B=100°,
∴∠BOA=80°,
∵OE平分∠BOF,
∴∠BOE=∠EOF,又∵∠FOC=∠AOC,
∴∠EOF+∠FOC= (∠BOF+∠FOA)=
(∠BOF+∠FOA)= ∠BOA=40°;
∠BOA=40°;
(3)结论:∠OCB:∠OFB的值不发生变化.理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
(4)由(1)知:OB∥AC,
则∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
则∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEC=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=80°,
∴α=β=20°,
∴∠OCA=2α+β=40°+20°=60.
考点:1.平行线的判定与性质;2.角的计算;3.平移的性质.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源:2016届浙江省温州市六校七年级下学期期中联考数学试卷(解析版) 题型:选择题
下列计算正确的是 ( )
A.3a+2a=5a2 B.a3·2a2=2a6 C.a4÷a2=a3 D.(-3a3)2=9a6
查看答案和解析>>
科目:初中数学 来源:2016届浙江省七年级下学期期中考试数学试卷(解析版) 题型:选择题
下列各式中,能用平方差公式计算的有( )
① ; ②
; ②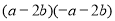 ;③
;③ ;④
;④ .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2016届浙江省台州市七年级下学期期中考试数学试卷(解析版) 题型:解答题
补全下列各题解题过程.(6分)
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.
证明:∵∠1=∠2(已知)
∠2=∠3 ∠1=∠4 ( )
∴∠3=∠4 ( 等量代换 )
∴_DB__∥_____ ( )
∴∠C=∠ABD ( )
∵∠C=∠D ( 已 知 )
∴∠D=∠ABD( )
∴DF∥AC( )

查看答案和解析>>
科目:初中数学 来源:2016届河南平顶山华英学校七年级下学级第一次月考数学试卷(解析版) 题型:解答题
先化简,再求值:
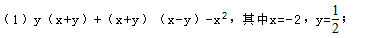
(2)(x+y)2-2x(x+y),其中x=3,y=2.
查看答案和解析>>
科目:初中数学 来源:2016届河北省邢台市沙河市七年级下学期期末数学试卷(解析版) 题型:选择题
下列长度的各组线段能组成一个直角三角形的是( )
A.4cm,6cm,11cm B.4cm,5cm,1cm
C.3cm,4cm,5cm D.2cm,3cm,6cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com