
【题目】如图,在等边三角形ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM.以下说法:①AD=AM,②DE=ME,③CN=![]() EC,④S△ABD=S△ACM中,正确的是_____.
EC,④S△ABD=S△ACM中,正确的是_____.

【答案】①③④
【解析】
证明△ABD≌△ACE(SAS),得出AD=AE,∠BAD=∠CAE,由折叠的性质得△ACM≌△ACE,得出△ABD≌△ACM,S△ABD=S△ACM,故④正确;由全等三角形的性质和折叠的性质得出AD=AE=AM,故①正确,证出∠CEN=30°,得出CN=![]() EC,故③正确;当∠DAE=30°或DM⊥AE时,DE=ME,故②错误;即可得出答案.
EC,故③正确;当∠DAE=30°或DM⊥AE时,DE=ME,故②错误;即可得出答案.
解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠ACE=∠BAC=60°,
在△ABD和△ACE中, ,
,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
由折叠的性质得:△ACM≌△ACE,
∴△ABD≌△ACM,
∴S△ABD=S△ACM,故④正确;
∵△ACM≌△ACE,
∴AE=AM,CE=CM,∠ACE=∠ACM,
∴AD=AE=AM,故①正确,
∴AC垂直平分线段EM,
∵∠ECN=60°,∠CNE=90°,
∴∠CEN=30°,
∴CN=![]() EC,故③正确;
EC,故③正确;
当∠DAE=30°或DM⊥AE时,DE=ME,故②错误;
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
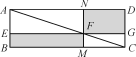
(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),
S矩形EBMF=S△ABC-(______________+______________).
易知,S△ADC=S△ABC,______________=______________,______________=______________.
可得S矩形NFGD=S矩形EBMF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若S四边形BFDE=9,则AB的长为:
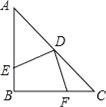
A. 3 B. 6 C. 9 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P.
(1)求证:AD=BE;
(2)设∠BPD=α,那么α的大小是否随D、E的位置变化而变化?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,D是BC的中点,动点E在边AB上(点E不与点A,B重合), 动点F在射线AC上,连结DE, DF.
(1)如图1,当∠DEB=∠DFC=90°时,直接写出DE与DF的数量关系;

(2)如图2,当∠DEB+∠DFC=180°(∠DEB≠∠DFC)时,猜想DE与DF的数量关系,并证明;

(3)当点E,D,F在同一条直线上时,
①依题意补全图3;
②在点E运动的过程中,是否存在EB=FC? ( 填“存在”或“不存在” ).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com