Question

【题目】如图，△ABC为等边三角形，AE＝CD，AD交BE于点P．

（1）求证：AD＝BE；

（2）设∠BPD＝α，那么α的大小是否随D、E的位置变化而变化？

Answer 1

【答案】（1）详见解析；（2）α的大小不随D、E的位置变化．

【解析】

（1）欲证AD＝BE，只要证明△ACD≌△BEA即可，根据等边三角形的性质可知AC＝AB，∠C＝∠BAC，结合已知条件，可利用SAS证得△ACD≌△BEA；

（2）结合（1）由α＝∠ABE+∠BAP＝∠CAD+∠BAP，即可得出结论．

解：（1）证明：∵△ABC为等边三角形，

∴AC＝AB，∠C＝∠BAC＝60°，

在△ACD和△BAE中，

，

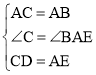∴△ACD≌△BEA（SAS）．

∴AD＝BE．

（2）不变．

理由：由（1）可知：△ACD≌△BEA，

∴∠CAD＝∠ABE，

∵α＝∠ABE+∠BAP＝∠CAD+∠BAP＝60°．

所以α的大小不随D、E的位置变化．