
【题目】已知关于x的方程![]() ①和
①和![]() ②问是否存在这样的n值,使方程①的两个实数根的差的平方等于方程②的一整数根?若存在,求出这样的n值;若不存在,请说明理由.
②问是否存在这样的n值,使方程①的两个实数根的差的平方等于方程②的一整数根?若存在,求出这样的n值;若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P.
(1)求证:AD=BE;
(2)设∠BPD=α,那么α的大小是否随D、E的位置变化而变化?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,D是BC的中点,动点E在边AB上(点E不与点A,B重合), 动点F在射线AC上,连结DE, DF.
(1)如图1,当∠DEB=∠DFC=90°时,直接写出DE与DF的数量关系;

(2)如图2,当∠DEB+∠DFC=180°(∠DEB≠∠DFC)时,猜想DE与DF的数量关系,并证明;

(3)当点E,D,F在同一条直线上时,
①依题意补全图3;
②在点E运动的过程中,是否存在EB=FC? ( 填“存在”或“不存在” ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方体盒子的棱长为2,BC的中点为M.
(1)一只蚂蚁从点M沿正方体的棱爬到点D1,蚂蚁爬行的最短路程是多少?
(2)若蚂蚁从点M沿正方体的表面爬行到点D1,请你结合正方体的展开图画出蚂蚁爬行的最短路线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有库存1800套旧桌凳,修理后捐助贫困山区学校.现有甲,乙两个木工组都想承揽这项业务.经协商后得知:甲木工组每天修理的桌凳套数是乙木工组每天修理桌凳套数的![]() ,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
(1)求甲,乙两木工组单独修理这批桌凳的天数;
(2)现有三种修理方案供选择:方案一,由甲木工组单独修理这批桌凳;方案二,由乙木工组单独修理这批桌凳;方案三,由甲,乙两个木工组共同合作修理这批桌凳.请计算说明哪种方案学校付的修理费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
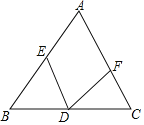
【题目】如图,已知在△ABC中,AB=AC,D为BC上一点,BE=CD,CF=BD,那么∠EDF等于( )
A.90°﹣∠AB.90°﹣![]() ∠AC.45°﹣
∠AC.45°﹣![]() ∠AD.180°﹣∠A
∠AD.180°﹣∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,顶点A、B、C都在正方形方格交点上,正方形方格的边长为1.
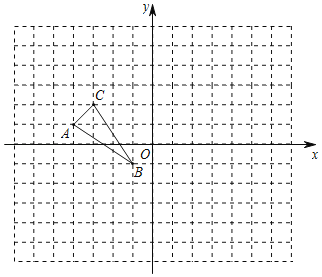
(1)写出A、B、C的坐标;
(2)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(3)在y轴上找到一点D,使得CD+BD的值最小,(在图中标出D点位置即可,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com