【题目】如图所示，在正方形网格上有6个三角形：①△ABC；②△BCD；③△BDE；④△BFG；⑤△FGH；⑥△EFK.其中②～⑥中与①相似的是( )
A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
津桥教育计算小状元系列答案科目：初中数学 来源： 题型：
【题目】如图，ΔP1OA1，ΔP2A1A2是等腰直角三角形，点P1、P2在函数y=
(x>0)的图象上，斜边OA1、A1A2都在x轴上，则点A2的坐标是____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道：x2﹣6x＝(x2﹣6x+9)﹣9＝(x﹣3)2﹣9；﹣x2+10＝﹣(x2﹣10x+25)+25＝﹣(x﹣5)2+25，这一种方法称为配方法，利用配方法请解以下各题：
(1)按上面材料提示的方法填空：a2﹣4a＝ ＝ ．﹣a2+12a＝ ＝ ．
(2)探究：当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值？请说明理由．
(3)应用：如图．已知线段AB＝6，M是AB上的一个动点，设AM＝x，以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB＝AC，点D在边BC上，点E在边AC上，且AD＝AE．
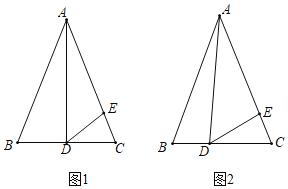
（1）如图1，当AD是边BC上的高，且∠BAD＝30°时，求∠EDC的度数；
（2）如图2，当AD不是边BC上的高时，请判断∠BAD与∠EDC之间的关系，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解学生的安全意识情况，在全校范围内随机抽取部分学生进行问卷调查，根据调查结果，把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次，并绘制成如图9的两幅尚不完整的统计图．
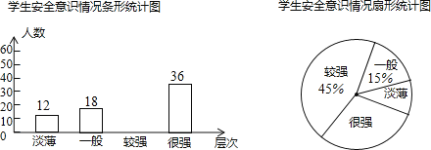
根据以上信息，解答下列问题：
（1）这次调查一共抽取了 名学生；
（2）请将条形统计图补充完整；
（3）分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是某同学对多项式（x2﹣4x+2）（x2﹣4x+6）+4进行因式分解的过程
解：设x2﹣4x＝y，
原式＝（y+2）（y+6）+4 （第一步）
＝y2+8y+16 （第二步）
＝（y+4）2（第三步）
＝（x2﹣4x+4）2（第四步）
（1）该同学第二步到第三步运用了因式分解的 （填序号）．
A．提取公因式 B．平方差公式
C．两数和的完全平方公式 D．两数差的完全平方公式
（2）该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？ ．（填“是”或“否”）如果否，直接写出最后的结果 ．
（3）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x+2）+1进行因式分解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在长方形ABCD中，边AB、BC的长（AB＜BC）是方程x2﹣7x+12=0的两个根．点P从点A出发，以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动，运动时间为t（秒）．
（1）求AB与BC的长；
（2）当点P运动到边BC上时，试求出使AP长为
时运动时间t的值；
（3）当点P运动到边AC上时，是否存在点P，使△CDP是等腰三角形？若存在，请求出运动时间t的值；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
