
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE。求证:△ABC是等腰三角形.

【答案】证明见解析.
【解析】
过点D作DG∥AC交BC于点G,根据平行线的性质可得出∠GDF=∠E、∠DGB=∠ACB,结合DF=EF以及∠DFG=∠EFC可证出△GDF≌△CEF(ASA),根据全等三角形的性质可得出GD=CE,结合BD=CE可得出BD=GD,进而可得出∠B=∠DGB=∠ACB,由此即可证出△ABC是等腰三角形.
过点D作DG∥AC交BC于点G,如图所示.
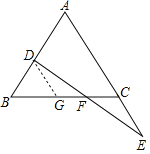
∵DG∥AC,
∴∠GDF=∠E,∠DGB=∠ACB.
在△GDF和△CEF中,
 ,
,
∴△GDF≌△CEF(ASA),
∴GD=CE.
∵BD=CE,
∴BD=GD,
∴∠B=∠DGB=∠ACB,
∴AB=AC
∴△ABC是等腰三角形.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
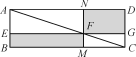
(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),
S矩形EBMF=S△ABC-(______________+______________).
易知,S△ADC=S△ABC,______________=______________,______________=______________.
可得S矩形NFGD=S矩形EBMF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P.
(1)求证:AD=BE;
(2)设∠BPD=α,那么α的大小是否随D、E的位置变化而变化?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,BC=2,直线l是长方形ABCD的一条对称轴,且分别与AD,BC交于点E,F,若直线l上的动点P,使得△PAB和△PBC均为等腰三角形.则动点P的个数有_______个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,D是BC的中点,动点E在边AB上(点E不与点A,B重合), 动点F在射线AC上,连结DE, DF.
(1)如图1,当∠DEB=∠DFC=90°时,直接写出DE与DF的数量关系;

(2)如图2,当∠DEB+∠DFC=180°(∠DEB≠∠DFC)时,猜想DE与DF的数量关系,并证明;

(3)当点E,D,F在同一条直线上时,
①依题意补全图3;
②在点E运动的过程中,是否存在EB=FC? ( 填“存在”或“不存在” ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方体盒子的棱长为2,BC的中点为M.
(1)一只蚂蚁从点M沿正方体的棱爬到点D1,蚂蚁爬行的最短路程是多少?
(2)若蚂蚁从点M沿正方体的表面爬行到点D1,请你结合正方体的展开图画出蚂蚁爬行的最短路线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com