Question

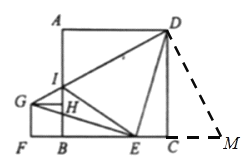
【题目】如图，点E是正方形ABCD的边BC上一点，连接DE，将DE绕着点E逆时针旋转90°，得到EG，过点G作GF⊥CB，垂足为F，GH⊥AB，垂足为H，连接DG，交AB于I．

（1）求证：四边形BFGH是正方形；

（2）求证：ED平分∠CEI；

（3）连接IE，若正方形ABCD的边长为3，则△BEI的周长为 　　．

Answer 1

【答案】（1）见解析；（2）见解析；（3）6

【解析】

（1）先证根据∠F＝∠GHB＝∠ABF＝90°证得四边形BFGH为矩形，再证明△DCE≌△EFG进而可证得BF＝FG，根据有一组邻边相等的矩形是正方形即可得证；

（2）延长EC到点M，使得CM＝AI，连接DM，先证△ADI≌△CDM可得DI＝DM，∠ADI＝∠CDM，进而可证△EDM≌△EDI得∠DEI＝∠DEC，即可得证；

（3）由（2）可知IE＝EM＝EC＋CM＝EC＋AI，则△BEI的周长为BI＋BE＋IE＝BI＋BE＋EC＋AI＝AB＋BC，由此可求得答案．

（1）证明：∵将DE绕着点E逆时针旋转90°得到EG，

∴DE＝EG，∠DEG＝90°，

∴∠DEC＋∠GEF＝90°，

∵在正方形ABCD中

∴∠C＝∠ABC＝∠ABF＝90°，BC＝CD，

∴∠DEC＋∠CDE＝90°，

∴∠CDE＝∠GEF，

∵GF⊥CB，GH⊥AB，

∴∠F＝∠GHB＝90°，

∴∠F＝∠GHB＝∠ABF＝90°，

∴四边形BFGH为矩形，

在△DCE与△EFG中，

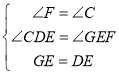
∴△DCE≌△EFG（AAS）

∴EF＝CD，FG＝CE，

∴EF＝BC，

∴EF－BE＝BC－BE，

即BF＝CE，

∴BF＝FG，

∴矩形BFGH为正方形；

（2）证明：如图，延长EC到点M，使得CM＝AI，连接DM，

∵在正方形ABCD中

∴∠ADC＝∠A＝∠DCE＝∠DCM＝90°，AD＝CD，

在△ADI与△CDM中，

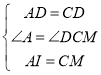
∴△ADI≌△CDM（SAS）

∴DI＝DM，∠ADI＝∠CDM，

∵DE＝EG，∠DEG＝90°，

∴∠EDG＝∠EGD＝45°，

又∵∠ADC＝90°，

∴∠ADI＋∠CDE＝45°，

∴∠EDM＝∠CDM＋∠CDE＝45°，

∴∠EDM＝∠EDG，

在△EDM与△EDI中，

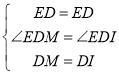
∴△EDM≌△EDI（SAS）

∴∠DEI＝∠DEC，

∴DE平分∠IEC；

（3）解：由（2）可知△EDM≌△EDI，

∴IE＝EM＝EC＋CM，

又∵CM＝AI，

∴IE＝EC＋CM＝EC＋AI，

∴△BEI的周长为BI＋BE＋IE＝BI＋BE＋EC＋AI＝AB＋BC，

∵正方形ABCD的边长为3，

∴△BEI的周长为AB＋BC＝6，

故答案为：6．