
 等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A,C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.
等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A,C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.分析 (1)由题可以看出P沿AB向右运动,Q沿BC向上运动,且速度都为1cm/s,S=$\frac{1}{2}$QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系;
(2)另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分条回答.
解答 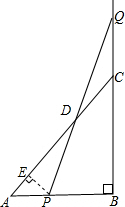 解:(1)过P点作PE⊥AC于E.
解:(1)过P点作PE⊥AC于E.
当t<10秒时,P在线段AB上,此时CQ=t,PB=10-t
∴s=$\frac{1}{2}$×t×(10-t)=$\frac{1}{2}$(10t-t2)
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t-10
∴s=$\frac{1}{2}$×t×(t-10)=$\frac{1}{2}$(t2-10t);
(2)∵S△ABC=$\frac{1}{2}$AB•BC=50,
∴当t<10秒时,S△PCQ=$\frac{1}{2}$(10t-t2)=50,
整理得t2-10t+100=0无解(6分)
当t>10秒时,S△PCQ=$\frac{1}{2}$(t2-10t)=50,
整理得t2-10t-100=0解得t=5±5$\sqrt{5}$(舍去负值),
∴当点P运动5+5$\sqrt{5}$秒时,S△PCQ=S△ABC.
点评 考查了一元二次方程的应用,做此类题应首先找出未知量与已知量的对应关系,利用已知量来表示未知量,许多问题就会迎刃而解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 5cm和7cm | B. | 20cm和30cm | C. | 8cm和16cm | D. | 6cm和10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| t(s) | 0.25 | 0.5 | 0.75 | 1 | 1.25 |
| V1(m/s) | 12 | 9 | 6 | 3 | 0 |
| S(m) | 3.375 | 6 | 7.875 | 9 | 9.375 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
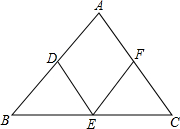 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,若添加一个条件,可以使四边形ADEF为菱形,你认为添加的条件可以是AB=AC.(只需要填写一个条件即可)
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,若添加一个条件,可以使四边形ADEF为菱形,你认为添加的条件可以是AB=AC.(只需要填写一个条件即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com