解:(1)解法一:∵一次函数y=kx-4k的图象与x轴交于点A,
∴点A的坐标为(4,0).
∵抛物线y=ax
2+bx+c经过O、A两点,
∴c=0,16a+4b=0.
∴b=-4a.
解法二:∵一次函数y=kx-4k的图象与x轴交于点A,
∴点A的坐标为(4,0).
∵抛物线y=ax
2+bx+c经过O、A两点,
∴抛物线的对称轴为直线x=2.
∴x=-

=2.
∴b=-4a.
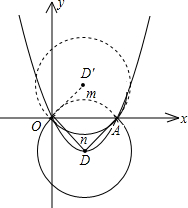
(2)由抛物线的对称性可知,DO=DA
∴点O在⊙D上,且∠DOA=∠DAO
又由(1)知抛物线的解析式为y=ax
2-4ax
∴点D的坐标为(2,-4a)
①当a>0时,如图
设⊙D被x轴分得的劣弧为
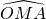
,它沿x轴翻折后所得劣弧为
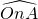
,显然
所在的圆与⊙D关于x轴对称,设它的圆心为D'
∴点D'与点D也关于x轴对称
∵点O在⊙D'上,且⊙D与OD'相切,
∴点O为切点
∴D'O⊥OD
∴∠DOA=∠D'OA=45°
∴△ADO为等腰直角三角形
∴OD=2

∴点D的纵坐标为-2
∴-4a=-2,
∴a=

,b=-4a=-2.
∴抛物线的解析式为y=

x
2-2x.
②当a<0时,
同理可得:OD=2

抛物线的解析式为y=-

x
2+2x
综上,⊙D半径的长为

,抛物线的解析式为y=

x
2-2x或y=-

x
2+2x.
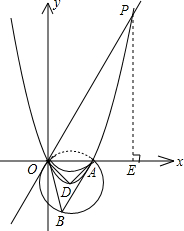
(3)答:抛物线在x轴上方的部分上存在点P,使得∠POA=

∠OBA
设点P的坐标为(x,y),且y>0
①当点P在抛物线y=

x
2-2x上时(如图)
∵点B是⊙D的优弧上的一点
∴∠OBA=

∠ADO=45°
∴∠POA=

∠OBA=60°
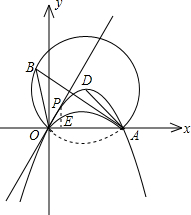
过点P作PE⊥x轴于点E,
∴tan∠POE=
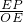
∴

=tan60°,
∴y=

.
由
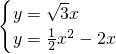
解得:
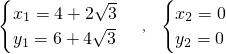
(舍去)
∴点P的坐标为
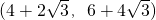
.
②当点P在抛物线y=-

x
2+2x上时(如图)
同理可得,y=

由
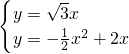
解得:
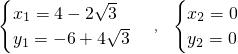
(舍去)
∴点P的坐标为(4-2

,-6+4

).
综上,存在满足条件的点P,点P的坐标为(4+2

,6+4

)或(4-2

,-6+4

).
分析:(1)根据图象,易得点A、C的坐标,代入解析式可得a、b的关系式;
(2)根据抛物线的对称性,结合题意,分a>0,a<0两种情况讨论,可得答案;
(3)根据题意,设出P的坐标,按P的位置不同分两种情况讨论,可得答案.
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.

 ∠OBA?若存在,求出点P的坐标;若不存在,请说明理由.
∠OBA?若存在,求出点P的坐标;若不存在,请说明理由.
 =2.
=2.
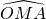 ,它沿x轴翻折后所得劣弧为
,它沿x轴翻折后所得劣弧为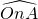 ,显然
,显然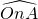 所在的圆与⊙D关于x轴对称,设它的圆心为D'
所在的圆与⊙D关于x轴对称,设它的圆心为D'
 ,b=-4a=-2.
,b=-4a=-2. x2-2x.
x2-2x.
 x2+2x
x2+2x ,抛物线的解析式为y=
,抛物线的解析式为y= x2-2x或y=-
x2-2x或y=- x2+2x.
x2+2x. ∠OBA
∠OBA x2-2x上时(如图)
x2-2x上时(如图) ∠ADO=45°
∠ADO=45° ∠OBA=60°
∠OBA=60°
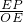
 =tan60°,
=tan60°, .
.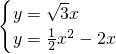
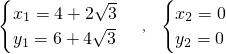 (舍去)
(舍去)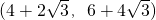 .
. x2+2x上时(如图)
x2+2x上时(如图)
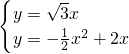
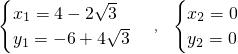 (舍去)
(舍去) ,-6+4
,-6+4 ).
). ,6+4
,6+4 )或(4-2
)或(4-2 ,-6+4
,-6+4 ).
).


 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=