
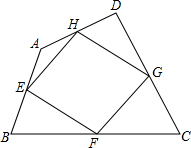
 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )| A. | S1=3S2 | B. | 2S1=3S2 | C. | S1=2S2 | D. | 3S1=4S2 |
分析 由E为AB中点,且EF平行于AC,EH平行于BD,得到△BEK与△ABM相似,△AEN与△ABM相似,利用面积之比等于相似比的平方,得到△EBK面积与△ABM面积之比为1:4,且△AEN与△EBK面积相等,进而确定出四边形EKMN面积为△ABM的一半,同理得到四边形MKFP面积为△MBC面积的一半,四边形QMPG面积为△DMC面积的一半,四边形MNHQ面积为△ADM面积的一半,四个四边形面积之和即为四个三角形面积之和的一半,即为四边形ABCD面积的一半.
解答 解: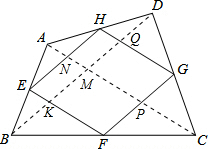 设AC与EH、FG分别交于点N、P,BD与EF、HG分别交于点K、Q,
设AC与EH、FG分别交于点N、P,BD与EF、HG分别交于点K、Q,
∵E是AB的中点,EF∥AC,EH∥BD,
∴△EBK∽△ABM,△AEN∽△EBK,
∴$\frac{{S}_{△EBK}}{{S}_{△ABM}}$=$\frac{1}{4}$,S△AEN=S△EBK,
∴$\frac{{S}_{四边形EKMN}}{{S}_{△ABM}}$=$\frac{1}{2}$,同理可得$\frac{{S}_{四边形KFPM}}{{S}_{△BCM}}$=$\frac{1}{2}$,$\frac{{S}_{四边形QGPM}}{{S}_{△DCM}}$=$\frac{1}{2}$,$\frac{{S}_{四边形HQMN}}{{S}_{△DAM}}$=$\frac{1}{2}$,
∴$\frac{{S}_{四边形EFGH}}{{S}_{四边形ABCD}}$=$\frac{1}{2}$,
∴四边形ABCD的面积为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是S1=2S2.
故选:C.
点评 此题主要考查了中点四边形以及相似三角形的判定与性质等知识,熟练应用三角形中位线的性质是解题关键.


科目:初中数学 来源: 题型:选择题
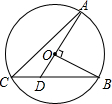 如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )
如图,OA,OB是⊙O的半径,且OA⊥OB,AO的延长线与弦BC交于点D,连结AC.若∠B=25°,则∠A的度数是( )| A. | 65° | B. | 45° | C. | 25° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
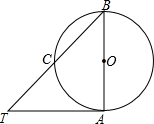 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | B. | $\frac{-x+y}{x+y}$=-1 | C. | $\frac{(n-m)^{3}}{(m-n)^{2}}$=n-m | D. | $\frac{a}{b}$=$\frac{am}{bm}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com