
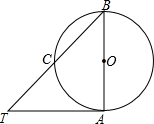
 如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.
如图,AB是⊙O的直径,AT为⊙O的切线,∠ABT=45°,则下列结论中正确的有( )①∠T=45°;②AT=BA;③∠TAB=90°;④点C为BT中点.| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
分析 由切线的性质可知AB⊥AT,所以∠TAB=90°,再结合已知条件可求出∠T=45°;因为∠T=∠B,所以可得AT=BA,连接AC,由等腰直角三角形的性质可得点C为BT中点,问题得解.
解答 解:连接AC,
∵AB是⊙O的直径,AT为⊙O的切线,
∴AB⊥AT,
∴∠TAB=90°,故③正确;
∵∠ABT=45°,
∴∠T=45°,故①正确;
∵∠T=∠B,
∴AT=BA,故②正确;
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC⊥BT,
又∵AT=AB,
∴BC=TC,
即点C为BT中点,故④正确.
故选C.
点评 此题主要考查了切线的性质定理,是中考中常见问题,解题的关键是连接AC,利用等腰三角形的“三线合一”性质得到点C是BT中点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
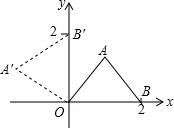 将等腰直角三角形AOB按图放置,然后绕O点逆时针旋转90°至A′OB′位置,点B(2,0),则A的坐标( )
将等腰直角三角形AOB按图放置,然后绕O点逆时针旋转90°至A′OB′位置,点B(2,0),则A的坐标( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | (-1,1) | D. | ($-\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
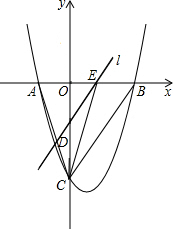 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
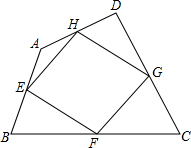 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )| A. | S1=3S2 | B. | 2S1=3S2 | C. | S1=2S2 | D. | 3S1=4S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)(x=2)=(x+2)(x-1) | B. | m2-1=(m+1)(m-1) | ||
| C. | x2+1=x(x+$\frac{1}{x}$) | D. | a(a-b)(b+1)=(a2-ab)(b+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com