练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．下列从左到右的变形，是因式分解的是（　　）
    A．（x-1）（x=2）=（x+2）（x-1）B．m2-1=（m+1）（m-1）
    C．x2+1=x（x+$\frac{1}{x}$）D．a（a-b）（b+1）=（a2-ab）（b+1）

    分析 根据因式分解是把一个多项式转化成几个整式积的形式，可得答案．

    解答 解：A、是乘法交换律，故A错误；
    B、把一个多项式转化成几个整式积的形式，故B正确；
    C、没把一个多项式转化成几个整式积的形式，故C错误；
    D、整式的乘法，故D错误．
    故选：B．

    点评 本题考查了因式分解的意义，因式分解是把一个多项式转化成几个整式积的形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．如图是一数值转换机，若输入的x为-4，则输出的结果为10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在学习“用直尺和圆规作一个角等于已知角”时，教科书介绍如下：

    作法：
    （1）如图所示，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
    （2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
    （3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；
    （4）过点D′画射线O′B′，则∠A′O′B′=∠AOB
    对于“想一想”中的问题，下列回答正确的是（　　）
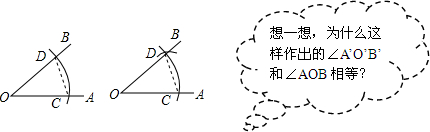
    A．根据“边边边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
    B．根据“边角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
    C．根据“角边角”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
    D．根据“角角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．已知一个两位数，个位上的数字比十位上的数字少4，这个两位数十位和个位交换位置后，新两位数与原两位数的积为1612，那么原数中较大的两位数是（　　）
    A．95B．59C．26D．62

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

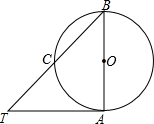    3．如图，AB是⊙O的直径，AT为⊙O的切线，∠ABT=45°，则下列结论中正确的有（　　）①∠T=45°；②AT=BA；③∠TAB=90°；④点C为BT中点．
    A．①②B．①②③C．①②③④D．①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．读语句画图，再填空，如图：
    （1）画直线AB，线段AC，射线BC；
    （2）取线段AC的中点D，连接BD；
    （3）图中以B为端点的线段有3条．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，在△ABC中，AB=AC，点D在AC边的右侧，连接DA、DB、DC，若AD=DC，∠ADB=∠ACB，AD=5，BD=11，则BC边的长为$\frac{24}{5}$$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知数轴上A，B两点对应数分别为a和b，且a、b满足等式（a+9）2+|7-b|=0，P为数轴上一动点，对应数为x．
    （1）求线段AB的长．
    （2）数轴上是否存在P点，使PA=3PB？若存在，求出x的值；若不存在，请说明理由．
    （3）在（2）的条件下，若点M、点N分别是线段AB，PB的中点，试求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列事件中，是随机事件的是（　　）
    A．通常加热到100℃时，水沸腾
    B．度量三角形的外角和，结果是360°
    C．明天太阳从西边升起
    D．篮球队员在罚球线上投篮一次，未投中

    查看答案和解析>>

    同步练习册答案