
����Ŀ��Ϊ���������Լ��ˮ��ij�о����Ծ�����ˮ�շ�ʵ�С����ݼۡ�������ÿ����ˮ��������15��ʱ������15�֣������û������շѣ���ÿ����ˮ������15��ʱ����������ÿ�ֲ����г����շѣ�С����4��5�·ݵ���ˮ�����շ�������±���
�·� | ��ˮ�����֣� | ˮ�ѣ�Ԫ�� |
4 | 22 | 51 |
5 | 20 | 45 |
��1�������ÿ��ˮ�Ļ����ۺ��г��ۣ�
��2����ÿ����ˮ��Ϊn�֣�Ӧ��ˮ��ΪmԪ����д��m��n֮��ĺ�����ϵʽ��
��3��С����6�·ݵ���ˮ��Ϊ26�֣�������Ҫ��ˮ�Ѷ���Ԫ��
���𰸡���1��3Ԫ/�֣�2Ԫ/����2��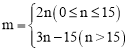 ��3��63Ԫ
��3��63Ԫ
���������⣺��1�����ݵ�ÿ����ˮ��������15��ʱ������15�֣������û������շѣ���ÿ����ˮ������15��ʱ����������ÿ�ֲ����г����շѣ�
��4�·���ˮ22�֣�ˮ��51Ԫ��5�·���ˮ20�֣�ˮ��45Ԫ��
���г����շѱ�Ϊ����51��45���£�22��20��=3��Ԫ/�֣���
��������շ�ΪxԪ/�֣�
��������ó���15x+��22��15����3=51����ã�x=2��
������ÿ��ˮ�Ļ����ۺ��г��۷ֱ�Ϊ��3Ԫ/�֣�2Ԫ/����
��2����n��15ʱ��m=2n����n��15ʱ��m=15��2+��n��15����3=3n��15��
��m��n֮��ĺ�����ϵʽΪ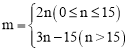 ��-
��-
��3����С����6�·ݵ���ˮ��Ϊ26�֣�
������Ҫ��ˮ��3��26��15=63Ԫ��
��1��������֪�ó�4�·���ˮ22�֣�ˮ��51Ԫ��5�·���ˮ20�֣�ˮ��45Ԫ������г����շѱ�Ϊ����51��45���£�22��20��=3��Ԫ/�֣��������ó�ÿ��ˮ�Ļ�������
��2�����ã�1��������ͬˮ�ۣ������õ�n��15ʱ��m=2n����n��15ʱ���ֱ����������
��3��������2��������ó�����ˮ��Ϊ26��ʱҪ��ˮ����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪OMƽ�֡�AOC��ONƽ�֡�BOC����AOB=90�㣬��BOC=30�㣮 ��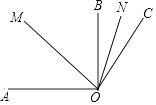
��1����AOC�Ķ�����
��2����MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC�ڽ��ڡ�O��P��BC�ϵ�һ�㣬��PB��PC��PA��BC��E����F��PC�ӳ����ϵĵ㣬CF=PB��AB=![]() ��PA=4��
��PA=4��
��1����֤����ABP�ա�ACF��
��2����֤��AC2=PAAE��
��3����PB��PC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ҹ��غ���һ�Ҳ����������ִ������ҹ�����,�Һ����ס�������Ѳ��ͧ���������13nmile��A��B��������ǰȥ���أ������Ӻ�ͬʱ����C�ؽ������أ���֪��Ѳ��ͧÿСʱ����120nmile����Ѳ��ͧÿСʱ����50nmile������Ϊ��ƫ��40�㣬�ʣ���Ѳ��ͧ�ĺ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ô���ʽ��ʾ��a��b������ƽ���ͼ�ȥ���dz˻���2��������ȷ���ǣ� ��
A.a2+b2��2ab
B.��a+b��2��2ab
C.a2b2��2ab
D.2��a2+b2��ab��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Լ����ϵ���ĸΪ�β���˳�����У���������һ��ͳ�ƣ�������һƪС���ģ����ݶ�������ĸa��b���ֵĻ�����ɺ�����������⣺
Two Trips
Jack brought a small plane and began to fly it�� He soon became excited and made his plane all kinds of tricks��
Jack had a friend��named Tom�� One day Jack said to him����I will pick you up in my plane������I will be glad to��'answered Tom�� They went up��and Jack flew around for half an hour and did all kinds of tricks in the air�� Then they came down�� Tom was to be back safely��and said to Jack����Well��Jack��thank you very much for those two trips in your plane����Jack was very surprised and asked����Two trips������Yes��my first and my last��'an��swered Tom��
�����������
������ĸ�ĸ��� | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
������ĸa��Ƶ�� | |||||||
������ĸa��Ƶ�� | |||||||
������ĸb��Ƶ�� | |||||||
������ĸb��Ƶ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧij���ѧ��ϲ�������������������ϲ����һ������������ͳ��ͼ���ָ�������˵����
�����ܻ�ӭ�������˶���ƹ����
����ϲ�������ѧ���ﵽ�༶ѧ��������![]() ��
��
����ϲ����ë���ѧ���ﵽ�༶ѧ��������![]() ��
��
������ȷ�Ľ���Ϊ��������
A.�٢�
B.�٢�
C.�ڢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�D��BC���ϵ�һ�㣬����AD��ȡAD���е�E������A��BC��ƽ������CE���ӳ��߽��ڵ�F������DF�� 
��1����֤��AF=DC��
��2�����ʣ�AD��CF����ʲô����ʱ���ı���AFDC�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com