练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    问题背景

    1.（1）如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点E作EF∥AB交BC于点F．请按图示数据填空：

    四边形DBFE的面积  ▲    ，

    △EFC的面积S1＝   ▲   ，

    △ADE的面积S2＝   ▲   ．

    探究发现

    2.（2）在（1）中，若，，DE与BC间的距离为．请证明S2＝4S1 S2．

    拓展迁移

    3.（3）如图2，平行四边形DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为2、5、3，试利用（2）中的结论求△ABC的面积．

     

     

    1.解: （1），，．       ……3分

    2.（2）证明：∵DE∥BC，EF∥AB，

    ∴四边形DBFE为平行四边形，，．∴△ADE∽△EFC．

    ∴．∵，     ∴．

    ∴．而，   ∴

    3.（3）解：过点G作GH∥AB交BC于H，则四边形DBHG为平行四边形．

    ∴，，．

    ∵四边形DEFG为平行四边形，∴． 

    ∴．∴．    

    ∴△DBE≌△GHF．∴△GHC的面积为．

    由（2）得，平行四边形DBHG的面积为．

    ∴△ABC的面积为．

    解析:略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
    精英家教网精英家教网
    ①如图1，在正三角形ABC中，M，N分别是AC，AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN；
    ②如图2，在正方形ABCD中，M，N分别是CD，AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
    然后运用类比的思想提出了如下命题；
    ③如图3，在正五边形ABCDE中，M，N分别是CD，DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN．任务要求：
    （1）请你从①，②，③三个命题中选择一个进行证明；
    （2）请你继续完成下面的探索：
    ①如图4，在正n（n≥3）边形ABCDEF…中，M，N分别是CD，DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM=CN成立；（不要求证明）
    ②如图5，在正五边形ABCDE中，M，N分别是DE，AE上的点，BM与CN相交于点O，若∠BON=108°时，试问结论BM=CN是否还成立．若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

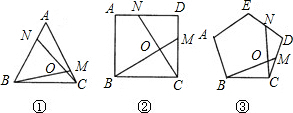
    （2011•临川区模拟）问题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．
    问题探究：
    （1）①如图1所示，当G在CD边上时，猜想线段BG、DE的数量关系及所在直线的位置关系．（不要求证明）
    ②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，请选择图2或图3证明你的判断．
    类比研究：
    （2）若将原题中的“正方形”改为“矩形”（如图4所示），且
    AB
    BC
    =
    CE
    CG
    =k（其中k＞0），请直接写出线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断．
    拓展应用：
    （3）在（1）中图2中，连接DG、BE，若AB=3，EF=2，求BE2+DG2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

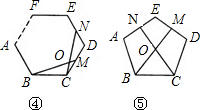
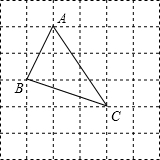    问题背景：“在△ABC中，AB、BC、AC三边的长分别为
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积．”
    小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网络中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），
    （1）如图所示．这样不需求△ABC的高，而借用网格就能计算出它的面积是
    3.5
    3.5
    ．
    （2）如图我们把上述求面积的方法叫做构图法．若△DCE三边的长分别为
    		m2+16n2
    、
    		9m2+4n2
    、
    		4m2+4n2
    （m＞0，n＞0，且m≠n），试运用构图法求出这三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年浙江省金华地区九年级下学期第一次月考数学卷 题型：解答题

    问题背景

    1.（1）如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点E作EF∥AB交BC于点F．请按图示数据填空：

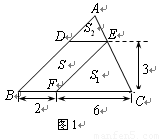
    四边形DBFE的面积  ▲    ，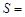

    △EFC的面积S1＝   ▲   ，

    △ADE的面积S2＝   ▲   ．

    探究发现

    2.（2）在（1）中，若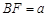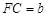，，DE与BC间的距离为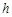．请证明S2＝4S1 S2．

    拓展迁移

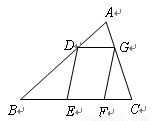
    3.（3）如图2，平行四边形DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为2、5、3，试利用（2）中的结论求△ABC的面积．

     

    查看答案和解析>>

    同步练习册答案