
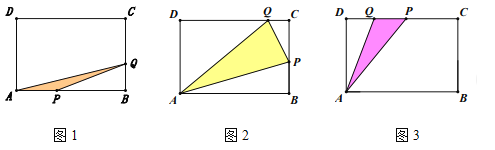
【题目】如图1,长方形![]() 中,
中,![]() 点
点![]() 从点
从点![]() 出发,沿
出发,沿![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 恰好到达点
恰好到达点![]() ,已知点
,已知点![]() 每秒比点
每秒比点![]() 每秒多运动
每秒多运动![]() 当其中一点到达
当其中一点到达![]() 时,另一点停止运动.
时,另一点停止运动.
![]() 求
求![]() 两点的运动速度;
两点的运动速度;
![]() 当其中一点到达点
当其中一点到达点![]() 时,另一点距离
时,另一点距离![]() 点
点 ![]() (直接写答案);
(直接写答案);
![]() 设点
设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的面积
的面积![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.

【答案】(1)点![]() 的运动速度是
的运动速度是![]() ,则
,则![]() 的运动速度为
的运动速度为![]() ;(2)
;(2)![]() ;(3)
;(3)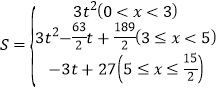 .
.
【解析】
(1)设点P的运动速度是xcm/s,则Q的运动速度为(x-1)cm/s,根据“当点P到达点B时,点Q恰好到达点C”列方程求解即可;
(2)先求出点P到达D的时间和点Q到达D的时间,判断出点Q先到达D.根据P离D的距离为=(9+6+9)-P已经走过的路程,即可得到结论.
(3)分三种情况讨论即可:①当0<x<3时;②当3≤t<5时;③当5≤x≤![]() 时.
时.
(1)设点P的运动速度是xcm/s,则Q的运动速度为(x-1)cm/s.
![]()
方程两边同乘x(x-1),得9(x-1)=6x.
解得:x=3.
检验:当x=3时,x(x-1)≠0.
所以,原分式方程的解是x=3.符合题意.
Q的运动速度=3-1=2(cm/s).
答:点P的运动速度是3cm/s,则Q的运动速度为2cm/s.
(2)∵AB=CD=9,BC=AD=6,点P到达D的时间t=(9+6+9)÷3=8(秒),点Q到达D的时间t=(6+9)÷2=7.5(秒),∴点Q先到达D.当Q达到D时,P离D的距离为:(9+6+9)-7.5×3=1.5(cm).
(3) ①当0<x<3时,如图1.
![]()
②当3≤t<5时,如图2.
∵BP=3t-9,CP=9+6-3t-9=15-3t.CQ=2t-6,DQ=6+9-2t=15-2t,AD=6,∴![]()
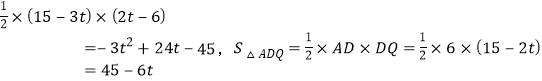 .
.
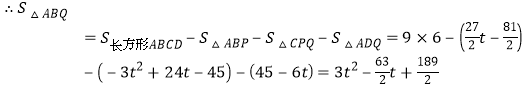 .
.
③当![]() 时,如图3.
时,如图3.
∵QC=2t-6,PC=3t-15,∴PQ=(2t-6)-(3t-15)=-t+9.
∴![]()
综上所述: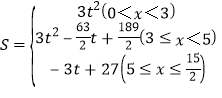


科目:初中数学 来源: 题型:
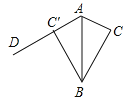
【题目】如图,△ABC的面积为6,AC3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的![]() 处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.6
B.13
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )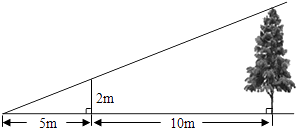
A.5m
B.6m
C.7m
D.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
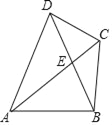
【题目】如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面三个图形中∠P和∠A,∠C的关系,请你从所得三个关系中任意选出一个,说明你探究结论的正确性.
结论:(1)___________________;
(2)____________________;
(3)_____________________;
(4)选择结论____________,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com