
【题目】如图,已知AB∥CD,分别探究下面三个图形中∠P和∠A,∠C的关系,请你从所得三个关系中任意选出一个,说明你探究结论的正确性.
结论:(1)___________________;
(2)____________________;
(3)_____________________;
(4)选择结论____________,说明理由.

【答案】(1)∠APC+∠PAB+∠PCD=360°;(2)∠APC=∠PAB+∠PCD;(3)∠PCD=∠APC+∠PAB;(4)∠APC+∠PAB+∠PCD=360°,理由见解析.
【解析】
(1)过点P作PE∥AB,则AB∥PE∥CD,再根据两直线平行,同旁内角互补即可解答;
(2)过点P作PF∥AB,则AB∥CD∥PF,再根据两直线平行,内错角相等即可解答;
(3)根据AB∥CD,可得出∠1=∠PCD,再根据三角形外角的性质进行解答;
(4)选择以上结论任意一个进行证明即可.
解:(1)过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°.
故答案为:∠APC+∠PAB+∠PCD=360°;
(2)过点P作直线PF∥AB,
∵AB∥CD,
∴AB∥PF∥CD,
∴∠PAB=∠1,∠PCD=∠2,
∴∠APC=∠PAB+∠PCD.
故答案为:∠APC=∠PAB+∠PCD;
(3)∵AB∥CD,
∴∠1=∠C,
∵∠1=∠PAB+∠APC,
∴∠PCD=∠APC+∠PAB.
故答案为:∠PCD=∠APC+∠PAB.
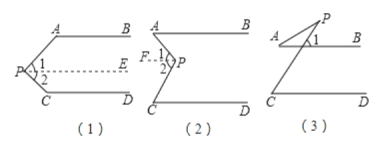
(4)选择结论∠APC+∠PAB+∠PCD=360°
理由:过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°
故答案为:∠APC+∠PAB+∠PCD=360°.


科目:初中数学 来源: 题型:
【题目】如图1,长方形![]() 中,
中,![]() 点
点![]() 从点
从点![]() 出发,沿
出发,沿![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 恰好到达点
恰好到达点![]() ,已知点
,已知点![]() 每秒比点
每秒比点![]() 每秒多运动
每秒多运动![]() 当其中一点到达
当其中一点到达![]() 时,另一点停止运动.
时,另一点停止运动.
![]() 求
求![]() 两点的运动速度;
两点的运动速度;
![]() 当其中一点到达点
当其中一点到达点![]() 时,另一点距离
时,另一点距离![]() 点
点 ![]() (直接写答案);
(直接写答案);
![]() 设点
设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的面积
的面积![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
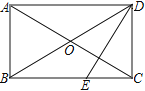
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
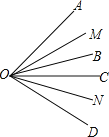
(1)若∠BOC=25°,∠MOB=15°,∠NOD=10°,求∠AOD的大小;
(2)若∠AOD=75°,∠MON=55°,求∠BOC的大小;
(3)若∠AOD=α,∠MON=β,求∠BOC的大小(用含α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=10cm,在直线AB上取一点C,使AC=16cm,则线段AB的中点与AC的中点的距离为( )
A.13cm或26cmB.6cm或13cmC.6cm或25cmD.3cm或13cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB.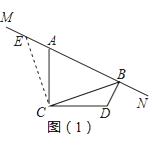
(1)问题发现
如图(1),过点C作CE⊥CB,与MN交于点E,则易发现BD和EA之间的数量关系为 , BD、AB、CB之间的数量关系为 .
(2)拓展探究
当MN绕点A旋转到如图(2)位置时,BD、AB、CB之间满足怎样的数量关系?请写出你的猜想,并给予证明.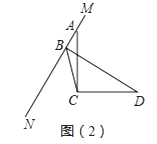
(3)解决问题
当MN绕点A旋转到如图(3)位置时(点C、D在直线MN两侧),若此时∠BCD=30°,BD=2时,CB= . 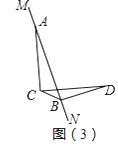
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′ 分别为EF、EG、GF的中点,如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com