
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)先化简,再求值:(![]() )
)![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3) -7;(4)
;(3) -7;(4)![]() ;
;![]()
【解析】
(1)根据二次根式加减法运算的法则运算即可,二次根式的加减一般可以分三步进行,①将每一个二次根式化成最简二次根式;②找出其中的同类二次根式;③合并同类二次根式.(2)利用平方差公式和完全平方公式计算;(3)根据零指数幂、负整数指数幂和绝对值的意义化简计算即可;(4)首先把分式化简,先算括号里面的减法,再算括号外的除法,化简后,再代入x、y的值即可.
解:(1)原式=![]() +
+![]() -
- ![]() +3
+3![]() =
=![]() ;
;
(2)原式=20-50-(5-2![]() +2)
+2)
=-30-7+2![]()
=-37+2![]() ;
;
(3)原式=1+![]() -4-3
-4-3![]() -4=-7;
-4=-7;
(4)解:(![]() )÷
)÷![]()
=[ ![]() ]×
]×![]()
=( ![]() )×
)×![]()
=![]() ×
×![]()
=![]() ×
×![]()
=![]() ,
,
当![]() 时,原式=
时,原式=![]()


科目:初中数学 来源: 题型:
【题目】如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )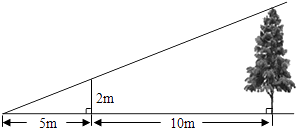
A.5m
B.6m
C.7m
D.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与因式分解:
(1)计算:
①![]() ;②(﹣2x﹣y)(y﹣2x)﹣(2x+y)2;
;②(﹣2x﹣y)(y﹣2x)﹣(2x+y)2;
(2)因式分解:
①2x2﹣4x+2;②a2(x﹣y)+9b2(y﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,高铁列车座位后面的小桌板收起时可以近似地看作与地面垂直,展开小桌板后,桌面会保持水平,其中图1、图2分别是小桌板收起时和展开时的实物,图3中的实线是小桌板展开后的示意图,其中OB表示小桌板桌面的宽度,BC表示小桌板的支架,连接OA,此时OA=75厘米,∠AOB=∠ACB=37°,且支架长BC与桌面宽OB的长度之和等于OA的长度,求点B到AC的距离.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)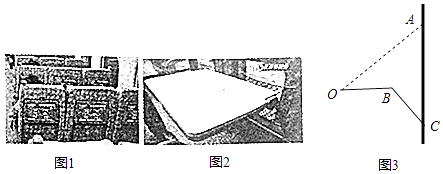
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
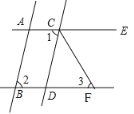
(1)试判断直线AE与BF有怎样的位置关系,并说明理由;
(2)若∠1=80°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探究下面三个图形中∠P和∠A,∠C的关系,请你从所得三个关系中任意选出一个,说明你探究结论的正确性.
结论:(1)___________________;
(2)____________________;
(3)_____________________;
(4)选择结论____________,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是A,B,C,D三点,按如下步骤作图:①先分别以A,B两点为圆心,以大于 ![]() AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于
AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于 ![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )
的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )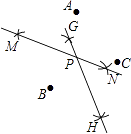
A.100°
B.120°
C.132°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: ![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73.)
≈1.73.)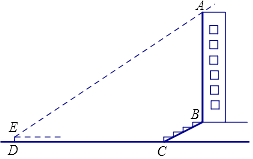
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com