
ЎҫМвДҝЎҝТСЦӘЎПACD=90ЎгЈ¬AC=DCЈ¬MNКЗ№эөгAөДЦұПЯЈ¬№эөгDЧчDBЎНMNУЪөгBЈ¬Б¬ҪУCBЈ®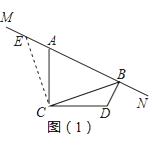
ЈЁ1Ј©ОКМв·ўПЦ
ИзНјЈЁ1Ј©Ј¬№эөгCЧчCEЎНCBЈ¬УлMNҪ»УЪөгEЈ¬ФтТЧ·ўПЦBDәНEAЦ®јдөДКэБҝ№ШПөОӘ Ј¬ BDЎўABЎўCBЦ®јдөДКэБҝ№ШПөОӘ Ј®
ЈЁ2Ј©НШХ№МҪҫҝ
өұMNИЖөгAРэЧӘөҪИзНјЈЁ2Ј©О»ЦГКұЈ¬BDЎўABЎўCBЦ®јдВъЧгФхСщөДКэБҝ№ШПөЈҝЗлРҙіцДгөДІВПлЈ¬ІўёшУиЦӨГчЈ®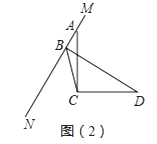
ЈЁ3Ј©ҪвҫцОКМв
өұMNИЖөгAРэЧӘөҪИзНјЈЁ3Ј©О»ЦГКұЈЁөгCЎўDФЪЦұПЯMNБҪІаЈ©Ј¬ИфҙЛКұЎПBCD=30ЎгЈ¬BD=2КұЈ¬CB= Ј® 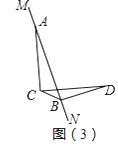
Ўҫҙр°ёЎҝ
ЈЁ1Ј©BD=AE,BD+AB= ![]() CB
CB
ЈЁ2Ј©ҪвЈәЦӨГчЈәИзНј2Ј¬№эөгCЧчЎНCBҪ»MNУЪөгEЈ¬
ЎЯЎПACD=90ЎгЈ¬
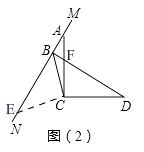
ЎаЎПACE=90Ўг+ЎПACBЈ¬ЎПBCD=90Ўг+ЎПACBЈ¬
ЎаЎПACE=ЎПBCDЈ¬
ЎЯDBЎНMNЈ¬
ЎаЎПCAE=90Ўг©ҒЎПAFBЈ¬ЎПD=90Ўг©ҒЎПCFDЈ¬
ЎЯЎПAFB=ЎПCFDЈ¬
ЎаЎПCAE=ЎПDЈ¬
ЎЯAC=DCЈ¬
ЎаЎчACEЎХЎчDCBЈ¬
ЎаAE=DBЈ¬CE=CBЈ¬
ЎЯЎПECB=90ЎгЈ¬
ЎаЎчECBКЗөИСьЦұҪЗИэҪЗРОЈ¬
ЎаBE= ![]() CBЈ¬
CBЈ¬
ЎаBE=AE©ҒAB=DB©ҒABЈ¬
ЎаBD©ҒAB= ![]() CBЈ»
CBЈ»
ЈЁ3Ј©![]() ©Ғ
©Ғ ![]()
ЎҫҪвОцЎҝҪвЈәЈЁ1Ј©ИзНј1Ј¬№эөгCЧчЎНCBҪ»MNУЪөгEЈ¬
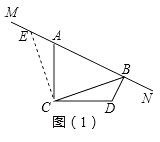
ЎЯЎПACD=90ЎгЈ¬
ЎаЎПACE=90Ўг©ҒЎПACBЈ¬ЎПBCD=90Ўг©ҒЎПACBЈ¬
ЎаЎПACE=ЎПBCDЈ¬
ЎЯDBЎНMNЈ¬
ЎаФЪЛДұЯРОACDBЦРЈ¬ЎПBAC+ЎПACD+ЎПABD+ЎПD=360ЎгЈ¬
ЎаЎПBAC+ЎПD=180ЎгЈ¬
ЎЯЎПCE+ЎПBAC=180ЎгЈ¬
ЎПCAE=ЎПDЈ¬
ЎЯAC=DCЈ¬
ЎаЎчACEЎХЎчDCBЈ¬
ЎаAE=DBЈ¬CE=CBЈ¬
ЎЯЎПECB=90ЎгЈ¬
ЎаЎчECBКЗөИСьЦұҪЗИэҪЗРОЈ¬
ЎаBE= ![]() CBЈ¬
CBЈ¬
ЎаBE=AE+AB=DB+ABЈ¬
ЎаBD+AB= ![]() CBЈ»
CBЈ»
ЛщТФҙр°ёКЗЈәBD=AEЈ¬BD+AB= ![]() CBЈ»ЈЁ3Ј©ИзНј3Ј¬№эөгCЧчЎНCBҪ»MNУЪөгEЈ¬
CBЈ»ЈЁ3Ј©ИзНј3Ј¬№эөгCЧчЎНCBҪ»MNУЪөгEЈ¬
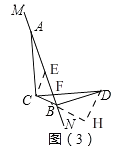
ЈЁ3Ј©ЎЯЎПACD=90ЎгЈ¬
ЎаЎПACE=90Ўг©ҒЎПDCEЈ¬
ЎПBCD=90Ўг©ҒЎПDCEЈ¬
ЎаЎПACE=ЎПBCDЈ¬
ЎЯDBЎНMNЈ¬
ЎаЎПCAE=90Ўг©ҒЎПAFCЈ¬ЎПD=90Ўг©ҒЎПCFDЈ¬
ЎЯЎПAFB=ЎПBFDЈ¬
ЎаЎПCAE=ЎПDЈ¬
ЎЯAC=DCЈ¬
ЎаЎчACEЎХЎчDCBЈ¬
ЎаAE=DBЈ¬CE=CBЈ¬
ЎЯЎПECB=90ЎгЈ¬
ЎаЎчECBКЗөИСьЦұҪЗИэҪЗРОЈ¬
ЎаBE= ![]() CBЈ¬
CBЈ¬
ЎаBE=AB©ҒAE=AB©ҒDBЈ¬
ЎаAB©ҒDB= ![]() CBЈ»
CBЈ»
ЎЯЎчBCEОӘөИСьЦұҪЗИэҪЗРОЈ¬
ЎаЎПBEC=ЎПCBE=45ЎгЈ¬
ЎЯЎПABD=90ЎгЈ¬
ЎаЎПDBH=45Ўг
№эөгDЧчDHЎНBCЈ¬
ЎаЎчDHBКЗөИСьЦұҪЗИэҪЗРОЈ¬
ЎаBD= ![]() BH=2Ј¬
BH=2Ј¬
ЎаBH=DH= ![]() Ј¬
Ј¬
ФЪRtЎчCDHЦРЈ¬ЎПBCD=30ЎгЈ¬DH= ![]() Ј¬
Ј¬
ЎаCH= ![]() DH=
DH= ![]() ЎБ
ЎБ ![]() =
= ![]() Ј¬
Ј¬
ЎаBC=CH©ҒBH= ![]() ©Ғ
©Ғ ![]() Ј»
Ј»
ЛщТФҙр°ёКЗЈә ![]() ©Ғ
©Ғ ![]() Ј®
Ј®
Ўҫҝјөгҫ«ОцЎҝёщҫЭМвДҝөДТСЦӘМхјюЈ¬АыУГ№ҙ№Й¶ЁАнөДёЕДоәНҪвЦұҪЗИэҪЗРОөДПа№ШЦӘК¶ҝЙТФөГөҪОКМвөДҙр°ёЈ¬РиТӘХЖОХЦұҪЗИэҪЗРОБҪЦұҪЗұЯaЎўbөДЖҪ·ҪәНөИУЪРұұЯcөДЖҪ·Ҫ,јҙ;a2+b2=c2Ј»ҪвЦұҪЗИэҪЗРОөДТАҫЭЈәўЩұЯөД№ШПөa2+b2=c2Ј»ўЪҪЗөД№ШПөЈәA+B=90ЎгЈ»ўЫұЯҪЗ№ШПөЈәИэҪЗәҜКэөД¶ЁТеЈ®(ЧўТвЈәҫЎБҝұЬГвК№УГЦРјдКэҫЭәНіэ·Ё)Ј®


 ұёХҪЦРҝјә®јЩПөБРҙр°ё
ұёХҪЦРҝјә®јЩПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДұЯРОABCDЦРЈ¬ABЎНBCЈ¬¶ФҪЗПЯACЎўBDПаҪ»УЪөгEЈ¬EОӘBDЦРөгЈ¬ЗТADЈҪBDЈ¬ABЈҪ2Ј¬ЎПBACЈҪ30ЎгЈ¬ФтDCЈҪ_____Ј®
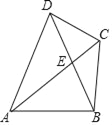
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘABЎОCDЈ¬·ЦұрМҪҫҝПВГжИэёцНјРОЦРЎПPәНЎПAЈ¬ЎПCөД№ШПөЈ¬ЗлДгҙУЛщөГИэёц№ШПөЦРИОТвСЎіцТ»ёцЈ¬ЛөГчДгМҪҫҝҪбВЫөДХэИ·РФЈ®
ҪбВЫЈәЈЁ1Ј©___________________Ј»
ЈЁ2Ј©____________________Ј»
ЈЁ3Ј©_____________________Ј»
ЈЁ4Ј©СЎФсҪбВЫ____________Ј¬ЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈРЛИӨРЎЧйПлІвБҝТ»ЧщҙуВҘABөДёЯ¶ИЈ®ИзНјЈ¬ҙуВҘЗ°УРТ»¶ОРұЖВBCЈ¬ТСЦӘBCөДіӨОӘ12ГЧЈ¬ЛьөДЖВ¶Иi=1Јә ![]() Ј®ФЪАлCөг40ГЧөДDҙҰЈ¬УГІвҪЗТЗІвөГҙуВҘ¶Ҙ¶ЛAөДСцҪЗОӘ37ЎгЈ¬ІвҪЗТЗDEөДёЯОӘ1.5ГЧЈ¬ЗуҙуВҘABөДёЯ¶ИФјОӘ¶аЙЩГЧЈҝЈЁҪб№ыҫ«И·өҪ0.1ГЧЈ©
Ј®ФЪАлCөг40ГЧөДDҙҰЈ¬УГІвҪЗТЗІвөГҙуВҘ¶Ҙ¶ЛAөДСцҪЗОӘ37ЎгЈ¬ІвҪЗТЗDEөДёЯОӘ1.5ГЧЈ¬ЗуҙуВҘABөДёЯ¶ИФјОӘ¶аЙЩГЧЈҝЈЁҪб№ыҫ«И·өҪ0.1ГЧЈ©
ЈЁІОҝјКэҫЭЈәsin37ЎгЎЦ0.60Ј¬cos37ЎгЎЦ0.80Ј¬tan37ЎгЎЦ0.75Ј¬ ![]() ЎЦ1.73Ј®Ј©
ЎЦ1.73Ј®Ј©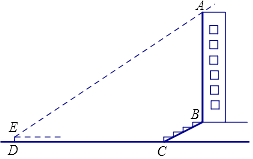
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,ЦұПЯABәНЦұПЯBCПаҪ»УЪөгB,Б¬ҪУAC,өгD. E. H·ЦұрФЪABЎўACЎўBCЙП,Б¬ҪУDEЎўDH,FКЗDHЙПТ»өг,ТСЦӘЎП1+ЎП3=180ЎгЈ¬
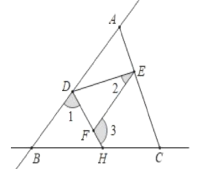
(1)ЗуЦӨЈәЎПCEF=ЎПEADЈ»
(2)ИфDHЖҪ·ЦЎПBDE,ЎП2=ҰБ,ЗуЎП3өД¶ИКэ.(УГҰБұнКҫ).
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРОABCDЦРЈ¬AB=4cmЈ¬AD=12cmЈ¬өгPФЪADұЯЙПТФГҝГл1cmөДЛЩ¶ИҙУөгAПтөгDФЛ¶ҜЈ¬өгQФЪBCұЯЙПЈ¬ТФГҝГл4cmөДЛЩ¶ИҙУөгCіц·ўЈ¬ФЪCBјдНщ·өФЛ¶ҜЈ¬БҪёцөгН¬Кұіц·ўЈ¬өұөгPөҪҙпөгDКұНЈЦ№ЈЁН¬КұөгQТІНЈЦ№Ј©Ј¬ФЪХв¶ОКұјдДЪЈ¬ПЯ¶ОPQУРЈЁЎЎЈ©ҙОЖҪРРУЪABЈҝ

A. 1 B. 2 C. 3 D. 4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘABCDЈ®
ЈЁ1Ј©ЧчНјЈ¬ЧчЎПAөДЖҪ·ЦПЯAEҪ»CDУЪөгEЈЁУГіЯ№жЧчНј·ЁЈ¬ұЈБфЧчНјәЫјЈЈ¬І»ТӘЗуРҙЧч·ЁЈ©Ј»
ЈЁ2Ј©ФЪЈЁ1Ј©өДМхјюПВЈ¬ЕР¶ПЎчAEDөДРОЧҙІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com