
【题目】解不等式组: 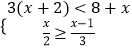 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
【答案】解:  ,
,
解不等式①得:x<1,
解不等式②得:x≥﹣2,
在数轴上表示不等式组的解集:
![]()
∴不等式组的解集是﹣2≤x<1.
【解析】解不等式①得:x<1,解不等式②得:x≥﹣2,用大小小大中间找得出解集,并把解集在数轴上表示出来。
【考点精析】掌握不等式的解集在数轴上的表示和一元一次不等式组的解法是解答本题的根本,需要知道不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB.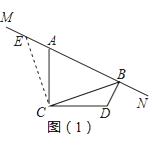
(1)问题发现
如图(1),过点C作CE⊥CB,与MN交于点E,则易发现BD和EA之间的数量关系为 , BD、AB、CB之间的数量关系为 .
(2)拓展探究
当MN绕点A旋转到如图(2)位置时,BD、AB、CB之间满足怎样的数量关系?请写出你的猜想,并给予证明.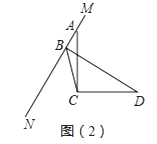
(3)解决问题
当MN绕点A旋转到如图(3)位置时(点C、D在直线MN两侧),若此时∠BCD=30°,BD=2时,CB= . 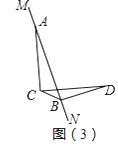
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标为(3,4),⊙A的半径为3,延长OA交⊙A于点B,过点B作⊙A的切线,交y轴于点C,则OC长为( )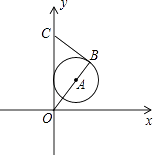
A.8
B.9
C.10
D.11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(8,0),点B的坐标为(6,4),点C的坐标为(0,4),点P从原点O出发,以每秒3的单位长度的速度沿x轴向右运动,点Q从点B出发,以每秒1的单位长度的速度沿线段BC向左运动,P,Q两点同时出发,当点Q运动到点C时,P,Q两点停止运动,设运动时间为t(秒).
(1)当t= 时,四边形OPQC为矩形;
(2)当t= 时,线段PQ平分四边形OABC的面积;
(3)在整个运动过程中,当以ACPQ为顶点的四边形为平行四边形时,求该平行四边形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′ 分别为EF、EG、GF的中点,如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用960元购进一批服装,并以每件46元的价格全部售完![]() 由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.
![]() 该服装店第一次购买了此种服装多少件?
该服装店第一次购买了此种服装多少件?
![]() 两次出售服装共盈利多少元?
两次出售服装共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com