
【题目】如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标为O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),若如图过点M(1,2)的直线MP(与y轴交于点P)将多边形OABCDE分割成面积相等的两部分,则直线MP的函数表达式是 . 
【答案】y= ![]() x+
x+ ![]()
【解析】解:延长CB交y轴于点F,
∵A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),
∴S正方形OABF=OAAB=2×2=4,
S矩形CDEF=CFCD=4×2=8,
∴S多边形OABCDE=4+8=12,
设直线PG的解析式为y=kx+b(k≠0),
∵M(1,2),
∴k+b=2①,
∵点P在y轴上,
∴P(0,b),
∵C(4,2),D(4,4),
∴G(4,4k+b),
∴S梯形PGDE= ![]() (DG+PE)DE=
(DG+PE)DE= ![]() S多边形OABCDE=
S多边形OABCDE= ![]() ×(4﹣4k﹣b+4﹣b)×4=6,即8k+4b=10②,
×(4﹣4k﹣b+4﹣b)×4=6,即8k+4b=10②,
①联立得, ![]() ,
,
解得 ![]() ,
,
故此一次函数的解析式为:y= ![]() x+
x+ ![]() .
.
故答案为:y= ![]() x+
x+ ![]() .
.
延长CB交y轴于点F,根据O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4)求出多边形OABCDE的面积,设直线PG的解析式为y=kx+b(k≠0),把点M代入即可得到k+b=2,再用k、b表示出P、G两点坐标,再由S梯形PGDE= ![]() S多边形OABCDE即可得出kb的值,故可得出结论.
S多边形OABCDE即可得出kb的值,故可得出结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
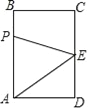
【题目】如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A﹣B﹣C﹣E运动,最终到达点E.若点P运动的时间为x秒,则当x=__时,△APE的面积等于5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2, ![]()
B.2,1
C.4, ![]()
D.4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是ABCD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( ) 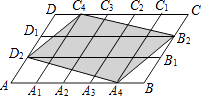
A.4
B.![]()
C.![]()
D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M. 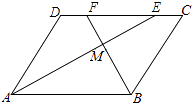
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=2ax2+ax-32经过点B.
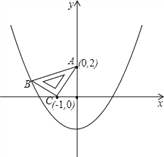
(1)写出点B的坐标;
(2)求抛物线的解析式;
(3)若三角板ABC从点C开始以每秒1个单位长度的速度向x轴正方向平移,求点A落在抛物线上时所用的时间,并求三角板在平移过程扫过的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com