Question

【题目】在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，且点A（0，2），点C（-1，0），如图所示：抛物线y=2ax2+ax-32经过点B．

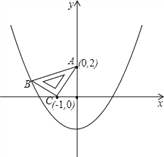
（1）写出点B的坐标；

（2）求抛物线的解析式；

（3）若三角板ABC从点C开始以每秒1个单位长度的速度向x轴正方向平移，求点A落在抛物线上时所用的时间，并求三角板在平移过程扫过的面积；

（4）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）B（-3，1）（2）y=x2+x-（3）8.5（4）（1，-1）

【解析】试题分析：（1）由于△ABC是等腰Rt△，若过B作BD⊥x轴于D，易证得△BCD≌△CAO，则BD=OA=2，BD=OC=1，即可求出B点坐标为：B（-3，1）．

（2）将B点坐标代入抛物线的解析式中，即可求出待定系数a的值，也就求得了抛物线的解析式．

（3）设平移后的三角形为△A′B′C′，由于是沿x轴正方向平移，所以A、A′的纵坐标不变，且A′在抛物线的图象上，由此可求出A′的坐标，即可求出AA′，CC′的距离，进而可求出平移过程所用的时间；

那么扫过部分的面积=△ABC的面积+?AA′C′C的面积．

（4）此题要分两种情况进行讨论：

①以C为直角顶点，AC为直角边；可求出直线BC的解析式，联立抛物线的解析式即可求出P点坐标，然后判断CP是否与AC相等即可．

②以A为直角顶点，AC为直角边，方法同①．

试题解析：（1）过B作BD⊥x轴于D；

∵∠BCA=90°，

∴∠BCD=∠CAO=90°-∠ACO；

又∵BC=AC，∠BDC=∠AOC=90°，

∴△BDC≌△COA；

∴AO=DC=2，BD=OC=1，

∴B（-3，1）．

（2）由于抛物线过B点，则有：2a×9+（-3）a-32=1，

解得a=

∴y=x2+x-．

（3）设平移后的三角形为△A′B′C′；

当y=2时，x2+x-=2

解得x=3（负值舍去）；

∴A′（3，2），C′（2，0）；

∴平移过程所用去的时间为3÷1=3秒；

S扫=S△ABC+S四边形AA′C′C=×（）2+3×2=8.5（平方单位）．

（4）①若以AC为直角边，C为直角顶点；

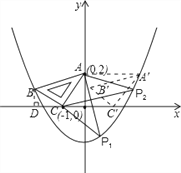
设直线BC交抛物线y=x2+x-于P1，

易求得直线BC的解析式为y=-x-；不难求得P1（1，-1），此时CP1=AC；

∴△ACP1为等腰直角三角形；

②若以AC为直角边，点A为直角顶点；

过A作AF∥BC，交抛物线y=x2+x-于P2，易求得直线AF的解析式为y=-x+2；

因为以AC为直角边，点A为直角顶点的等腰Rt△ACP的顶点P有两种情况，即AC=AP2，AC⊥AP2，

∵CO=1，AO=2，

只有P到y轴距离为2，到x轴距离为1，且在第一象限符合题意，

此时P2（2，1），

或者P点在第三象限P3（-2，3）符合题意，

经检验点P2（2，1）与P3（-2，3）不在抛物线上，

所以，符合条件的点P有1个：（1，-1）．