
【题目】抛物线![]() 的顶点在直线
的顶点在直线![]() 上,过点F
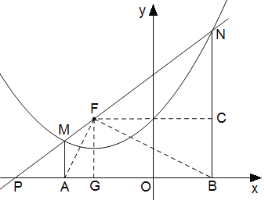
上,过点F![]() 的直线与抛物线交于M、N两点(点M在点N的左边),MA⊥
的直线与抛物线交于M、N两点(点M在点N的左边),MA⊥![]() 轴于点A,NB⊥
轴于点A,NB⊥![]() 轴于点B.
轴于点B.

(1)先通过配方求抛物线的顶点坐标(坐标可用含![]() 的代数式表示),再求
的代数式表示),再求![]() 的值;
的值;
(2)设点N的横坐标为![]() ,试用含
,试用含![]() 的代数式表示点N的纵坐标,并说明NF=NB;
的代数式表示点N的纵坐标,并说明NF=NB;
(3)若射线NM交![]() 轴于点P,且PA×PB=
轴于点P,且PA×PB=![]() ,求点M的坐标.
,求点M的坐标.
【答案】(1)顶点坐标为(-2 , ![]() ),
),![]() =2;(2)N(a,
=2;(2)N(a,![]() );(3)M(-3 ,
);(3)M(-3 ,![]() ).
).
【解析】
试题分析:(1)利用配方法将二次函数整理成顶点式即可,再利用点在直线上的性质得出答案即可;
(2)首先利用点N在抛物线上,得出N点坐标,再利用勾股定理得出NF2=NC2+FC2,进而得出NF2=NB2,即可得出答案;
(3)求点M的坐标,需要先求出直线PF的解析式.首先由(2)的思路得出MF=MA,然后连接AF、FB,通过证明△PFA∽△PBF,利用相关的比例线段将PAPB的值转化为PF的值,进而求出点F的坐标和直线PF的解析式,即可得解.
试题解析:(1)![]()
∴顶点坐标为(-2 , ![]() )
)
∵顶点在直线![]() 上,
上,
∴-2+3=![]() ,
,
得![]() =2
=2
(2)∵点N在抛物线上,
∴点N的纵坐标为![]()
即点N(a,![]() )
)
过点F作FC⊥NB于点C,
在Rt△FCN中,FC=![]() +2,NC=NB-CB=
+2,NC=NB-CB=![]() ,
,![]()
∴![]()
而![]() =
=![]() =
=![]()
∴![]() =
=![]() ,NF=NB
,NF=NB
(3)连结AF、BF
由NF=NB,得∠NFB=∠NBF,
由(2)的结论知,MF=MA,∴∠MAF=∠MFA,
∵MA⊥x轴,NB⊥x轴,∴MA∥NB,∴∠AMF+∠BNF=180°
∵△MAF和△NFB的内角总和为360°,
∴2∠MAF+2span>∠NBF=180°,∠MAF+∠NBF=90°
∵∠MAB+∠NBA=180°,
∴∠FBA+∠FAB=90°
又∵∠FAB+∠MAF=90°
∴∠FBA=∠MAF=∠MFA
又∵∠FPA=∠BPF,
∴△PFA∽△PBF,
∴![]()
过点F作FG⊥![]() 轴于点G,在Rt△PFG中,PG=
轴于点G,在Rt△PFG中,PG=![]() =
=![]() ,
,
∴PO=PG+GO=![]() ,
,
∴P(-![]() , 0)
, 0)
设直线PF:y=kx+b把点F(-2 , 2)、点P(-![]() , 0)代入y=kx+b
, 0)代入y=kx+b
解得![]() =
=![]() ,
,![]() =
=![]() ,
,
∴直线PF:![]()
解方程![]() ,得
,得![]() =-3或
=-3或![]() =2(不合题意,舍去)
=2(不合题意,舍去)
当![]() =-3时,
=-3时,![]() =
=![]() ,
,
∴M(-3 ,![]() )
)


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:
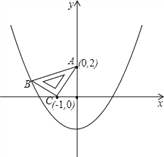
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=2ax2+ax-32经过点B.
(1)写出点B的坐标;
(2)求抛物线的解析式;
(3)若三角板ABC从点C开始以每秒1个单位长度的速度向x轴正方向平移,求点A落在抛物线上时所用的时间,并求三角板在平移过程扫过的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于角的说法正确的个数是( )
①角是由两条有公共端点的射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y= ![]() 的图象的两个交点.
的图象的两个交点. 
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com