
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).

(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
【答案】(1)y=-x2+![]() x+1;(2)4;(3)(
x+1;(2)4;(3)(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据题意得出B点坐标,再利用待定系数法求出抛物线解析式;
(2)首先表示出P,E点坐标,再利用PE=PD-ED,结合二次函数最值求法进而求出PE的最大值;
(3)根据题意可得:PE=BC,则-x2+4x=3,进而求出Q点的横坐标,再利用直线上点的坐标性质得出答案.
试题解析:(1)∵BC⊥x轴,垂足为点C(4,0),且点B在直线y=![]() x+1上,
x+1上,
∴点B的坐标为:(4,3),
∵抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴![]() ,
,
解得: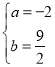 ,
,
故抛物线的解析式为:y=-x2+![]() x+1;
x+1;
(2)如图所示:设动点P的坐标为;(x,-x2+![]() x+1),
x+1),
则点E的坐标为:(x,![]() x+1),
x+1),
∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=(-x2+![]() x+1)-(
x+1)-(![]() x+1)
x+1)
=-x2+4x
=-(x-2)2+4,
则当x=2时,PE的最大值为:4;
(3)∵PC与BE互相平分,
∴PE=BC,
∴-x2+4x=3,即x2-4x+3=0,
解得:x1=1,x2=3,
∵点Q分别时PC,BE的中点,且点Q在直线y=![]() x+1,
x+1,
∴①当x=1时,点Q的横坐标为:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ),
),
②当x=3时,点Q的横坐标为:![]() ,
,
∴点Q的坐标为:(![]() ,
,![]() ),
),
综上所述,点Q的坐标为:(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】股市规定:股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.若一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
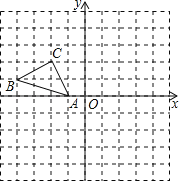
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)点B1的坐标为 ,点C2的坐标为 .
(3)△ABC经过怎样的旋转可直接得到△A1B2C2, .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD 中,AB=3,BC=4,E,F 是对角线 AC上的两个动点,分别从 A,C 同时出发, 相向而行,速度均为 1cm/s,运动时间为 t 秒,当其中一个动点到达后就停止运动.
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 始终是平行四边形.
(2)在(1)条件下,当 t 为何值时,四边形 EGFH 为矩形.
(3)若 G,H 分别是折线 A﹣B﹣C,C﹣D﹣A 上的动点,与 E,F 相同的速度同时出发,当 t 为何值时,四边形 EGFH 为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
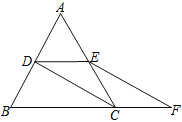
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连结CD和EF.
BC,连结CD和EF.
(1)求证:四边形CDEF是平行四边形;
(2)求四边形BDEF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com