
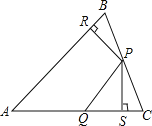
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB于点R,PS⊥AC于点S,若PR=PS,则下列结论正确的个数是( )
(1)PQ=PB; (2)AS=AR;(3)△BRP≌△PSC (4)∠C=∠SPC
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC,由直角三角形全等的判定方法得出Rt△ARP≌Rt△ASP,从而判断出(2)正确;根据由一组边相等和一组角相等无法判断△BRP≌△PSC,从而判断出(3)错误;同(3)也无法判断△BRP≌△PSQ,所以PQ≠PB,从而判断出(1)错误;△PSC是直角三角形,不一定是等腰直角三角形,所以∠C与∠SPC不一定相等,从而判断出(4)错误.
连接AP,
∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,![]() ,
,
∴Rt△ARP≌Rt△ASP,(HL),
∴AR=AS,∴(2)正确;
∵PR=PS,∠PRB=∠PSC=90°,
∴无法判断△BRP≌△PSC,故(3)错误;
∵∠PRB=∠PSQ=90°,PR=PS,
无法判断△BRP≌△PSQ,
∴PQ≠PB,故(1)错误;
∵△PSC是直角三角形,不一定是等腰直角三角形,
∴∠C与∠SPC不一定相等,故(4)错误;
故选:A.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,然后回答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,所以
是无理数,而无理数是无限不循环小数,所以![]() 的小数部分我们不可能全部写出来,由于
的小数部分我们不可能全部写出来,由于![]() 的整数部分是1,将
的整数部分是1,将![]() 减去它的整数部分,差就是它的小数部分,因此
减去它的整数部分,差就是它的小数部分,因此![]() 的小数部分可用
的小数部分可用![]() ﹣1表示.
﹣1表示.
由此我们得到一个真命题:如果![]() =x+y,其中x是整数,且0<y<1,那么x=1,y=
=x+y,其中x是整数,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
请解答下列问题:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= ,b= ;
=a+b,其中a是整数,且0<b<1,那么a= ,b= ;
(2)如果﹣![]() =c+d,其中c是整数,且0<d<1,那么c= ,d= ;
=c+d,其中c是整数,且0<d<1,那么c= ,d= ;
(3)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知平面直角坐标系中,点![]() ,
,![]() 满足
满足![]() .
.
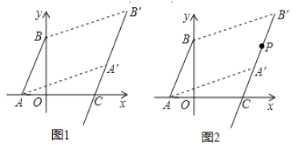
(1)求![]() 的面积;
的面积;
(2)将线段![]() 经过水平、竖直方向平移后得到线段
经过水平、竖直方向平移后得到线段![]() ,已知直线
,已知直线![]() 经过点
经过点![]() 的横坐标为5.
的横坐标为5.
①求线段![]() 平移过程中扫过的面积;
平移过程中扫过的面积;
②请说明线段![]() 的平移方式,并说明理由;
的平移方式,并说明理由;
③如图2,线段![]() 上一点
上一点![]() ,直接写出
,直接写出![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
(1)平面直角坐标系中,若点A(a,2a+1)在一次函数y=x-1的图像上,则a的值为___________;
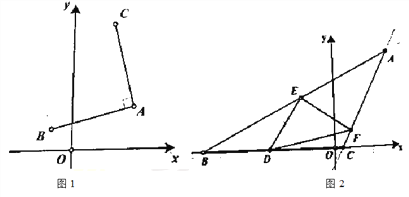
(2)如图1,平面直角坐标系中,已知A(4,2)、B(-1,1),若∠A=90°,点C在第一象限,且AB=AC,试求出C点坐标;
(3)近几年在经济、科技等多方面飞速发展的中国向世界展示了有一个繁华盛世.在政府的引导下,各地也都就本市特点修建了一些具有本地特色的旅游开发项目.如图2,某市就其地势特点,在一块由三条高速路(分别是x轴和直线AB:![]() 、直线AC:y=2x-1)围成的三角形区域内计划修建一个三角形的特色旅游小镇.如图,D(-4,0),△DEF的顶点E、F分别在线段AB、AC上,且∠DEF=90°,DE=EF,试求出该旅游小镇(△DEF)的面积.
、直线AC:y=2x-1)围成的三角形区域内计划修建一个三角形的特色旅游小镇.如图,D(-4,0),△DEF的顶点E、F分别在线段AB、AC上,且∠DEF=90°,DE=EF,试求出该旅游小镇(△DEF)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.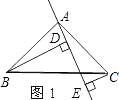
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.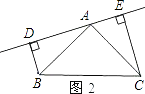
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数![]()
![]() 的图象经过点C.
的图象经过点C.
(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
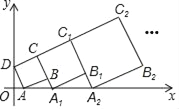
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com