
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2= . 
【答案】8
【解析】解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
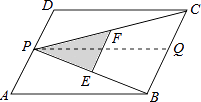
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF= ![]() BC,
BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=2,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=8.
所以答案是:8
【考点精析】利用三角形中位线定理和平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
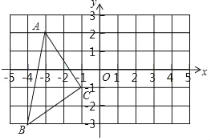
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°.
(1)尺规作图:作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)的条件下,连接BD,当BC=5cm,AB=13cm时,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.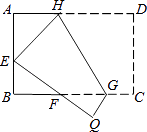
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB于点R,PS⊥AC于点S,若PR=PS,则下列结论正确的个数是( )
(1)PQ=PB; (2)AS=AR;(3)△BRP≌△PSC (4)∠C=∠SPC
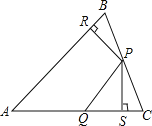
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com