【题目】如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是cm．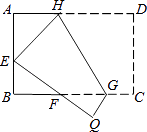
【答案】8
【解析】解：设AH=a，则DH=AD﹣AH=8﹣a，
在Rt△AEH中，∠EAH=90°，AE=4，AH=a，EH=DH=8﹣a，
∴EH2=AE2+AH2，即（8﹣a）2=42+a2，
解得：a=3．
∵∠BFE+∠BEF=90°，∠BEF+∠AEH=90°，
∴∠BFE=∠AEH．
又∵∠EAH=∠FBE=90°，
∴△EBF∽△HAE，
∴ 
= 
= 
= 
．
∵C△HAE=AE+EH+AH=AE+AD=12，
∴C△EBF= C△HAE=8．
所以答案是：8．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系中，
为坐标原点，点
的坐标为
，点
的坐标为
，点
的坐标为
，其中
满足方程组
．
（1）若点到
轴的距离为6，则
的值为_________；
（2）连接
，线段沿
轴方向向上平移到线段
，则点到直线
的距离为_______，线段扫过的面积为15，则点平移后对应点
的纵坐标为_______；
（3）连接，
，
，若
的面积小于等于12，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AD=2，AB=3，过点A，C作相距为2的平行线段AE，CF，分别交CD，AB于点E，F，则DE的长是（ ）
A.
B.
C.1
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们用[a]表示不大于a的最大整数，例如：[3.5]＝3，[4]＝4，[－1.5]＝－2；用{a}表示大于a的最小整数，例如：{3.5}＝4，{1}＝2，{－2.5}＝－2.解决下列问题：
(1)[－5.5]等于多少，{2.5}等于多少；
(2)若[x]＝3，写出x的取值范围；若{y}＝－2，写出y的取值范围．
(3)已知x，y满足方程组
，求x，y的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P为平行四边形ABCD边AD上一点，E、F分别为PB、PC的中点，△PEF、△PDC、△PAB的面积分别为S、S1、S2 ， 若S=2，则S1+S2= ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
(1)求出△ABC的面积；
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1；
(3)写出点A1，B1，C1的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于实数p，q，我们用符号min{p，q}表示p，q两数中较小的数，如min{1，2}=1，因此，min{﹣ 
，﹣ 
}=；若min{（x﹣1）2 ， x2}=1，则x= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则图中与∠DFM相等的角（不含它本身）的个数为（ ）
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合题
（1）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD=DE+CE．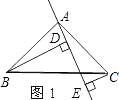
（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．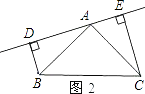
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com