
【题目】已知在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 满足方程组
满足方程组![]() .
.
(1)若点![]() 到
到![]() 轴的距离为6,则
轴的距离为6,则![]() 的值为_________;
的值为_________;
(2)连接![]() ,线段
,线段![]() 沿
沿![]() 轴方向向上平移到线段
轴方向向上平移到线段![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为_______,线段
的距离为_______,线段![]() 扫过的面积为15,则点
扫过的面积为15,则点![]() 平移后对应点
平移后对应点![]() 的纵坐标为_______;
的纵坐标为_______;
(3)连接![]() ,
,![]() ,
,![]() ,若
,若![]() 的面积小于等于12,求
的面积小于等于12,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)5;5;(3)
;(2)5;5;(3)![]() 且
且![]()
【解析】
(1)利用点到坐标轴的距离的特点即可求出d的值;
(2)根据方程组求出a-b=5,进而根据平移的性质,得出AA'=BB',再用面积公式即可求出点![]() 到直线
到直线![]() 的距离和点B沿
的距离和点B沿![]() 轴方向向上平移后B'的纵坐标;
轴方向向上平移后B'的纵坐标;
(3)分四种情况,利用面积的和差表示出△ABC的面积,进而建立不等式求解即可.
解:(1)点C的坐标为(c,d)且到x轴的距离为6,
∴|d|=6,
∴d=±6,
故答案为:±6;
(2)如图1,
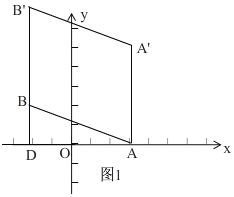
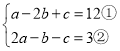
∴①+②得,3a-3b=15,
∴a-b=5,
∴b=a-5;
∴AD=a-b=5,即点![]() 到直线
到直线![]() 的距离为5,
的距离为5,
设平移后B的对应点B'(b,m),
∴AA'=BB'=|m-2|,
∵线段AB扫过的面积为15,
∴15=SAA'B'B=AA'×(a-b)=|m-2|×5
∴m=5或m=-1(向上平移,舍去),
∴平移后B点的坐标B'的纵坐标为5,
故答案为:5,5;
(3)由(2)可得,
2×②-①得,3a-3c=-6,
∴a-c=-2,
∴c=a+2,即AE=2,
如图2,

①当点C在x轴上方时,此时d>0,
过点B作BD⊥x轴于D,过点C作CF⊥x轴交x轴于E,BA的延长线于F,
∴BD∥EF,
∴△ADB∽△AEF,
![]() ,
,
![]() ,
,
∵DE=AD+AE=7,BD=2,C(c,d),
∴CE=d,
∴S△ABC=S梯形BDEC-S△ABD-S△ACE
![]()
![]()
![]()
![]()
![]()
∵△ABC的面积小于等于12,
∴0<S△ABC≤12,
![]() ,
,
∴![]()
又∵d>0,
∴![]() ;
;
②当点C在直线AB下方时,此时![]() ,如图3,
,如图3,
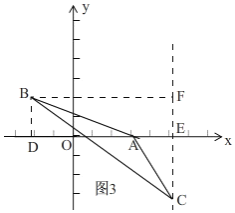
过点B作BD⊥x轴于D,过点C作CF⊥x轴交x轴于E,过点B作BF⊥CE于F,
S△ABC=S△BCF-S梯形AEFB-S△ACE
![]()
![]()
![]()
![]()
![]()
∵△ABC的面积小于等于12,
∴0<S△ABC≤12,
![]() ,
,
![]() ;
;
③当点C在直线AB上方,在x轴下方时,此时![]() ,如图4
,如图4
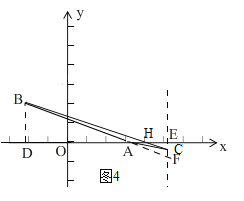
∵EF//BD,
∴△HBD∽△HCE,
∴![]() ,
,
设AH=m,则HE=2-m,HD=5+m,
∴![]() ,解得
,解得![]() ,
,
![]()
=![]()
=![]()
=![]()
=![]() ,
,
∵△ABC的面积小于等于12,
∴0<S△ABC≤12,
![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ;
;
④当C在直线AB上时,A、B、C不构成三角形,舍去,即![]() ,
,
当C在x轴上时,![]() ,符合题意,此时d=0,
,符合题意,此时d=0,
综上所述,d的取值范围为![]() 且
且![]() .
.


科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,已知![]() ,过点
,过点![]() 分别向
分别向![]() 轴作垂线,垂足分别是
轴作垂线,垂足分别是![]() ;
;
(1)点Q在直线![]() 上且与点P的距离为2,则点Q的坐标为__________
上且与点P的距离为2,则点Q的坐标为__________
(2)平移三角形![]() ,若顶点P平移后的对应点
,若顶点P平移后的对应点![]() ,画出平移后的三角形
,画出平移后的三角形![]() .
.
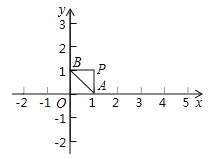
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某超市购买A、B、C三种商品.其中A、B两种商品的单价之和正好等于C商品的单价,小明前两次购买商品的数量和总费用如下表:
商品A的数量 | 商品B的数量 | 商品C的数量 | 总费用(元) | |
第一次 | 2 | 3 | 2 | 230 |
第二次 | 1 | 4 | 3 | 290 |
(1)求A、B、C三种商品的单价;
(2)若小明第三次需要购置A、B、C三种商品共m个,其中C商品的数量是A商品的数量的2倍,恰好花了480元钱.
①求m的最大值;
②若小明在第三次购买A,B,C三种商品时正好遇上“买一送一”活动,即购买一个C商品即可赠送一个A商品或一个B商品(优先赠送A商品),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
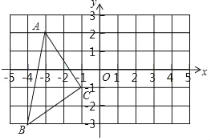
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
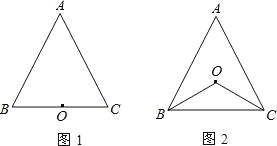
【题目】已知,点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)若点O点在△ABC的外部,△ABC是等腰三角形还成立吗?请画图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.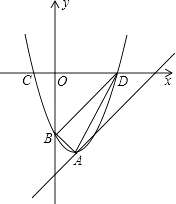
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.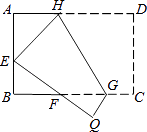
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com