
【题目】如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 . 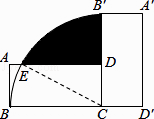
【答案】![]() π﹣2
π﹣2 ![]()
【解析】解:∵四边形ABCD是矩形, ∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CE=BC=4,
∴CE=2CD,
∴∠DEC=30°,
∴∠DCE=60°,
由勾股定理得:DE=2 ![]() ,
,
∴阴影部分的面积是S=S扇形CEB′﹣S△CDE= ![]() ﹣
﹣ ![]() ×2×2
×2×2 ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用扇形面积计算公式和旋转的性质对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() .
.
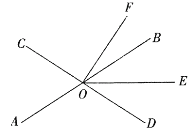
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() 平分
平分![]() ,∠BOF=12°,若设∠BOE=x°.
,∠BOF=12°,若设∠BOE=x°.
①则![]() = . (用含
= . (用含![]() 的代数式表示)
的代数式表示)
②求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明)
(3)如图3,写出∠BPD﹑∠B﹑∠D﹑∠BQD之间的数量关系?请证明你的结论.
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲同学用图3-①所示的方法作出了点C,表示数![]() ,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC.
(1)请说明甲同学这样做的理由;
(2)仿照甲同学的作法,在图3-②所给的数轴上描出表示-![]() 的点A.
的点A.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )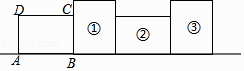
A.2017π
B.2034π
C.3024π
D.3026π
查看答案和解析>>
科目:初中数学 来源: 题型:
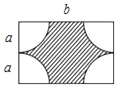
【题目】如图所示的是某居民小区的一块长为bm,宽为2am的长方形空地,为了美化环境,准备在这个长方形空地的四个顶点各修建一个半径为am的扇形花台,然后在花台内种花,其余空地种草,如果建筑花台及种花每平方米需要资金200元,种草每平方米需要资金150元,那么美化这块空地共需资金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( ) 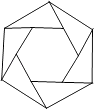
A.( ![]() )2016倍
)2016倍
B.( ![]() )2017倍
)2017倍
C.( ![]() )2018倍
)2018倍
D.( ![]() )2019倍
)2019倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com