
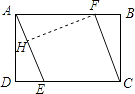
【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A.![]()
B.![]()
C.1
D.![]()
【答案】D
【解析】解:过F作FH⊥AE于H,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE,
∴DE=BF,
∴AF=3﹣DE,
∴AE= ![]() ,
,
∵∠FHA=∠D=∠DAF=90°,
∴∠AFH+∠HAF=∠DAE+∠FAH=90°,
∴∠DAE=∠AFH,
∴△ADE∽△AFH,
∴ ![]() ,
,
∴AE=AF,
∴ ![]() =3﹣DE,
=3﹣DE,
∴DE= ![]() ,
,
所以答案是:D.
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,已知![]() ,过点
,过点![]() 分别向
分别向![]() 轴作垂线,垂足分别是
轴作垂线,垂足分别是![]() ;
;
(1)点Q在直线![]() 上且与点P的距离为2,则点Q的坐标为__________
上且与点P的距离为2,则点Q的坐标为__________
(2)平移三角形![]() ,若顶点P平移后的对应点
,若顶点P平移后的对应点![]() ,画出平移后的三角形
,画出平移后的三角形![]() .
.
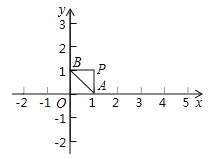
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.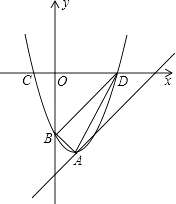
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°.
(1)尺规作图:作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)的条件下,连接BD,当BC=5cm,AB=13cm时,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D.下列四个命题:①当x>0时,y>0; ②若a=﹣1,则b=3;③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6 ![]() .其中正确的命题有( )个.
.其中正确的命题有( )个.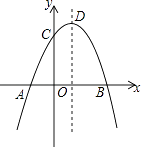
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.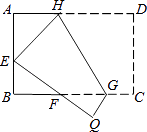
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
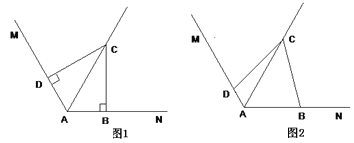
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com