
【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
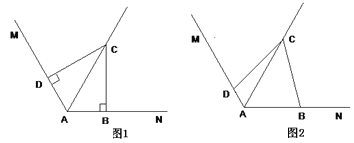
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)证明见解析(2) 成立,证明见解析
【解析】(1)证明: ∵∠MAN=120°,AC平分∠MAN.
∴∠DAC = ∠BAC =600
∵∠ABC=∠ADC=90°,
∴∠DCA=∠BCA=30°,
在Rt△ACD,Rt△ACB中,∠DCA=30°
∠BCA=30°
∴AC=2AD, AC = 2AB,
∴2AD=2AB
∴AD=AB
∴AD+AB=AC.
(2)解:(1)中的结论① DC = BC; ②AD+AB=AC都成立,
理由一:如图2,在AN上截取AE=AC,连结CE,
∵∠BAC =60°,
∴△CAE为等边三角形,
∴AC=CE,∠AEC =60°,
∵∠DAC =60°,∴∠DAC =∠AEC,
∵∠ABC+∠ADC=180°,∠ABC+∠EBC=180°,
∴∠ADC =∠EBC, ∴![]() ,
,
∴DC = BC,DA = BE, …
∴AD+AB=AB+BE=AE, ∴AD+AB=AC.
或者理由二:如图,过C作CE⊥AN,CF⊥AM于E、F

证明△BCE≌△DCF,得到
DC=BC,BE=DF
即AC=AE+AF=AB+AD亦可
得分参照理由一给分
(1)根据角平分线的性质可得∠DAC=∠BAC=60°,又已知∠ABC=∠ADC=90°,所以∠DCA=∠BCA=30°,根据直角三角形的性质可证AC=2AD,AC=2AB,所以AD+AB=AC.
(2)根据已知条件可在AN上截取AE=AC,连接CE,根据AAS可证△ADC≌△EBC,得到DC=BC,DA=BE,所以AD+AB=AB+BE=AE,即AD+AB=AC.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,然后回答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,所以
是无理数,而无理数是无限不循环小数,所以![]() 的小数部分我们不可能全部写出来,由于
的小数部分我们不可能全部写出来,由于![]() 的整数部分是1,将
的整数部分是1,将![]() 减去它的整数部分,差就是它的小数部分,因此
减去它的整数部分,差就是它的小数部分,因此![]() 的小数部分可用
的小数部分可用![]() ﹣1表示.
﹣1表示.
由此我们得到一个真命题:如果![]() =x+y,其中x是整数,且0<y<1,那么x=1,y=
=x+y,其中x是整数,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
请解答下列问题:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= ,b= ;
=a+b,其中a是整数,且0<b<1,那么a= ,b= ;
(2)如果﹣![]() =c+d,其中c是整数,且0<d<1,那么c= ,d= ;
=c+d,其中c是整数,且0<d<1,那么c= ,d= ;
(3)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知平面直角坐标系中,点![]() ,
,![]() 满足
满足![]() .
.
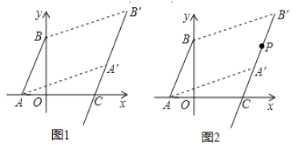
(1)求![]() 的面积;
的面积;
(2)将线段![]() 经过水平、竖直方向平移后得到线段
经过水平、竖直方向平移后得到线段![]() ,已知直线
,已知直线![]() 经过点
经过点![]() 的横坐标为5.
的横坐标为5.
①求线段![]() 平移过程中扫过的面积;
平移过程中扫过的面积;
②请说明线段![]() 的平移方式,并说明理由;
的平移方式,并说明理由;
③如图2,线段![]() 上一点
上一点![]() ,直接写出
,直接写出![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.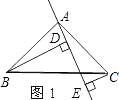
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.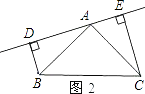
查看答案和解析>>
科目:初中数学 来源: 题型:
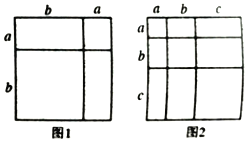
【题目】对于一个图形通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)根据整式乘法的运算法则,通过计算验证上述等a式;
(3)若a+b+c=l0,ab+ac+bc=35,利用得到的结论,求.![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com