
【题目】如图1,已知平面直角坐标系中,点![]() ,
,![]() 满足
满足![]() .
.
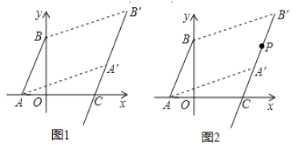
(1)求![]() 的面积;
的面积;
(2)将线段![]() 经过水平、竖直方向平移后得到线段
经过水平、竖直方向平移后得到线段![]() ,已知直线
,已知直线![]() 经过点
经过点![]() 的横坐标为5.
的横坐标为5.
①求线段![]() 平移过程中扫过的面积;
平移过程中扫过的面积;
②请说明线段![]() 的平移方式,并说明理由;
的平移方式,并说明理由;
③如图2,线段![]() 上一点
上一点![]() ,直接写出
,直接写出![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ;(2)①
;(2)①![]() 平行四边形
平行四边形![]() ;②线段
;②线段![]() 先向右平移7个单位,再向上平移2个单位得到线段
先向右平移7个单位,再向上平移2个单位得到线段![]() ,③
,③![]() .
.
【解析】
(1)利用非负数的性质求出a、b的值即可解决问题;
(2)①根据平移的性质得平行四边形![]() 与三角形
与三角形![]() 等底等高,再根据三角形面积公式求解即可;
等底等高,再根据三角形面积公式求解即可;
②过![]() 作
作![]() x轴于
x轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,垂足分别为
,垂足分别为![]() ,根据题意可设
,根据题意可设![]() ,由
,由![]() 三角形
三角形![]() 梯形
梯形![]() 平行四边形
平行四边形![]() 三角形
三角形![]() 三角形
三角形![]() 可列方程解出b值,从而可得结果;
可列方程解出b值,从而可得结果;
③利用待定系数法求出A′B′的表达式即可解决问题.
(1)![]() ,
,![]() .
.
![]() 且
且![]()
![]()
当![]() 时,
时,![]()
![]()
![]()
![]() ,
,![]()
![]() 三角形
三角形![]()
(2)①由平移性质可知,![]() ,
,![]()
点![]() 到
到![]() 的距离=点
的距离=点![]() 到
到![]() 的距离
的距离
故平行四边形![]() 与三角形
与三角形![]() 等底等高
等底等高
![]() 平行四边形
平行四边形![]() 三角形
三角形![]()
又三角形![]() 中,
中,![]() ,高
,高![]()
![]() 三角形
三角形![]()
![]() 平行四边形
平行四边形![]()
②过![]() 作
作![]() x轴于
x轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,垂足分别为
,垂足分别为![]()
由![]() 的横坐标为5,
的横坐标为5,![]() 的横坐标为
的横坐标为![]() 可知,线段
可知,线段![]() 平移规律是先向右移动了7个单位,
平移规律是先向右移动了7个单位,
不妨设![]()
![]() 三角形
三角形![]() 梯形
梯形![]() 平行四边形
平行四边形![]() 三角形
三角形![]() 三角形
三角形![]()
即![]() ,
,
解得:b=2,
由上可知,![]() (5,2),故线段
(5,2),故线段![]() 先向右平移7个单位,再向上平移2个单位得到线段
先向右平移7个单位,再向上平移2个单位得到线段![]() .
.
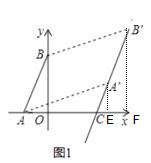
③![]() ,
,
∵![]() 在线段
在线段![]() 上,
上,![]() (5,2),B′(7,6),
(5,2),B′(7,6),
设直线A′B′的表达式为y=px+q,将A′和B′代入,
得![]() ,
,
解得:![]() ,
,
∴直线A′B′的表达式为y=2x-8,
∴m和n的关系式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
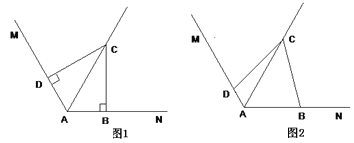
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要新建一个800平方米的长方形场地,且其长、宽的比为5:2.
(1)求这个长方形场地的长和宽为多少米?
(2)某个正方形场地的周围有一圈金属栅栏围墙,如果把原来面积为900平方米的正方形场地的栅栏围墙全部利用,来作为新场地的长方形围墙,栅栏围墙是否够用?为什么?(提示:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 . 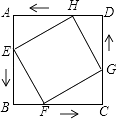
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB于点R,PS⊥AC于点S,若PR=PS,则下列结论正确的个数是( )
(1)PQ=PB; (2)AS=AR;(3)△BRP≌△PSC (4)∠C=∠SPC
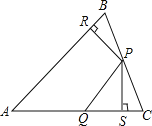
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
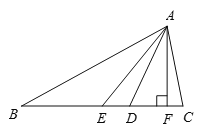
【题目】如图,在⊿ ABC中,AE是中线,AD是角平分线,AF是高,∠ B=30°, ∠ C=80°, BE=3,AF=2,填空:(1)AB= _________. (2)∠ BAD=________(3)∠ DAF=__________(4)S⊿ AEC=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
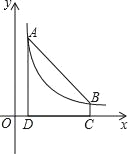
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连结AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com