
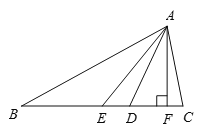
【题目】如图,在⊿ ABC中,AE是中线,AD是角平分线,AF是高,∠ B=30°, ∠ C=80°, BE=3,AF=2,填空:(1)AB= _________. (2)∠ BAD=________(3)∠ DAF=__________(4)S⊿ AEC=____________.
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知平面直角坐标系中,点![]() ,
,![]() 满足
满足![]() .
.
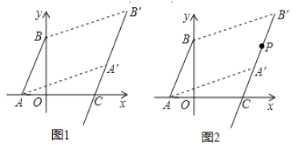
(1)求![]() 的面积;
的面积;
(2)将线段![]() 经过水平、竖直方向平移后得到线段
经过水平、竖直方向平移后得到线段![]() ,已知直线
,已知直线![]() 经过点
经过点![]() 的横坐标为5.
的横坐标为5.
①求线段![]() 平移过程中扫过的面积;
平移过程中扫过的面积;
②请说明线段![]() 的平移方式,并说明理由;
的平移方式,并说明理由;
③如图2,线段![]() 上一点
上一点![]() ,直接写出
,直接写出![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.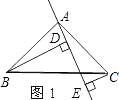
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.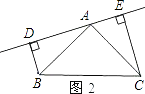
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2015次后,得到的等腰直角三角形的直角顶点P2016的坐标为( )
A.(4033,﹣1)
B.(4031,﹣1)
C.(4033,1)
D.(4031,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数![]()
![]() 的图象经过点C.
的图象经过点C.
(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上的一点,△PAD的面积恰好等于正方形ABCD的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
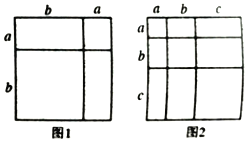
【题目】对于一个图形通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)根据整式乘法的运算法则,通过计算验证上述等a式;
(3)若a+b+c=l0,ab+ac+bc=35,利用得到的结论,求.![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:①乙工程队每天修公路240米;②甲工程队每天修公路120米;③甲比乙多工作6天;④A、B两地之间的公路总长是1680米.其中正确的说法有( )
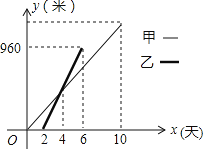
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com