
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2015次后,得到的等腰直角三角形的直角顶点P2016的坐标为( )
A.(4033,﹣1)
B.(4031,﹣1)
C.(4033,1)
D.(4031,1)
【答案】B
【解析】解:∵A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,
∴P1(1,1).
∵把△AP1B绕点B顺时针旋转180°,得到△BP2C1,
∴P2(3,﹣1).
同理可得出:P3(5,1),P4(7,﹣1),P5(9,1),…,
∴P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数).
∵2016=2×1008,
∴P2016(4031,﹣1).
故答案为:B.
根据在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,得到P1的坐标,由把△AP1B绕点B顺时针旋转180°,得到△BP2C1,得到P2的坐标,同理可得出P3,P4,P5,···,根据规律求出P2016的坐标.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 . 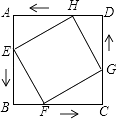
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点. 
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标. 注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊿ ABC中,AE是中线,AD是角平分线,AF是高,∠ B=30°, ∠ C=80°, BE=3,AF=2,填空:(1)AB= _________. (2)∠ BAD=________(3)∠ DAF=__________(4)S⊿ AEC=____________.
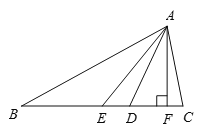
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究发现,地表以下岩层的温度与它所处的深度有表中所示的关系:
岩层的深度 | 1 | 2 | 3 | 4 | 5 | 6 | … |
岩层的温度 | 55 | 90 | 125 | 160 | 195 | 230 | … |
根据以上信息,回答下列问题:
(1)上表反映的两个变量之中,________是自变量,_______是因变量;
(2)岩层的深度![]() 每增加
每增加![]() ,温度
,温度![]() 是怎样变化的?试写出
是怎样变化的?试写出![]() 和
和![]() 的关系式;
的关系式;
(3)估计岩层![]() 深处的温度是多少?
深处的温度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
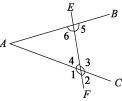
【题目】如图,(1)∠1,∠2,∠3,∠4,∠5,∠6是直线______,______被第三条直线_______所截而成的;
(2)∠2的同位角是______,∠1的同位角是 _________;
(3)∠3的内错角是______,∠4的内错角是 _________;
(4)∠6的同旁内角是______________,∠5的同旁内角是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
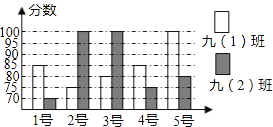
【题目】我区某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:
(1)九(1)班复赛成绩的中位数是 分,九(2)班复赛成绩的众数是 分;
(2)小明同学已经算出了九(1)班复赛的平均成绩![]() =85分;方差S2=
=85分;方差S2=![]() [(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
(3)根据(2)中计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com