
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点. 
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标. 注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() )
)
【答案】
(1)解:由点A(﹣1,0)和点B(3,0)得 ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)解:令x=0,则y=3,
∴C(0,3),
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4);
(3)解:设P(x,y)(x>0,y>0),
S△COE= ![]() ×1×3=
×1×3= ![]() ,S△ABP=
,S△ABP= ![]() ×4y=2y,
×4y=2y,
∵S△ABP=4S△COE,∴2y=4× ![]() ,
,
∴y=3,∴﹣x2+2x+3=3,
解得:x1=0(不合题意,舍去),x2=2,
∴P(2,3).
【解析】(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数b、c的值,进而可得到抛物线的对称轴方程;(2)令x=0,可得C点坐标,将函数解析式配方即得抛物线的顶点C的坐标;(3)设P(x,y)(x>0,y>0),根据题意列出方程即可求得y,即得D点坐标.
【考点精析】利用二次函数的性质和二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 当路程一定时,时间与速度成正比例
B. “全等三角形的面积相等”的逆命题是真命题
C. ![]() 是最简二次根式
是最简二次根式
D. 到直线AB的距离等于1厘米的点的轨迹是平行于直线AB且和AB距离为1cm的一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.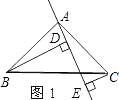
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.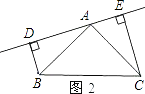
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2015次后,得到的等腰直角三角形的直角顶点P2016的坐标为( )
A.(4033,﹣1)
B.(4031,﹣1)
C.(4033,1)
D.(4031,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),与y轴相交于点C,动点M在线段OA和射线AC上运动.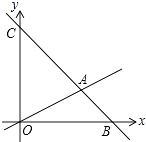
(1)求直线AB的解析式;
(2)若△OMC的面积是△OAC的面积的 ![]() ,请直接写出此时点M的坐标 .
,请直接写出此时点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com