
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

【答案】(1)y=﹣![]() ;(2)M(5,﹣
;(2)M(5,﹣![]() )或(﹣1,8).
)或(﹣1,8).
【解析】
(1)由Q(2,0),推出P(2,-4),利用待定系数法即可解决问题;
(2)根据三角形的面积公式求出MN的长,分两种情形求出点M的坐标即可.
(1)把x=2代入y=﹣2x得 y=﹣4
∴P(2,﹣4),
设反比例函数解析式y=![]() (k≠0),
(k≠0),
∵P在此图象上
∴k=2×(﹣4)=﹣8,
∴y=﹣![]() ;
;
(2)
∵P(2,﹣4),Q(2,0)
∴PQ=4,过M作MN⊥PQ于N.
则 ![]() PQMN=6,
PQMN=6,
∴MN=3,
设M(x,﹣![]() ),
),
则 x=2+3=5或x=2﹣3=﹣1
当x=5时,﹣![]() =﹣
=﹣![]() ,
,
当x=﹣1时,﹣![]() =1,
=1,
∴M(5,﹣![]() )或(﹣1,8).
)或(﹣1,8).
故答案为:(1)y=﹣![]() ;(2)M(5,﹣
;(2)M(5,﹣![]() )或(﹣1,8).
)或(﹣1,8).


科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(-2,2);C(2,-2).
为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(-2,2);C(2,-2).

(1) 请直接写出B点、C点、P点的对应点B1,C1,P1的坐标;
(2) 求△AOC的面积S△AOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
①![]() 的解x= .
的解x= .
②![]() 的解x= .
的解x= .
③![]() 的解x= .
的解x= .
④![]() 的解x= .
的解x= .
…
(1)根据你发现的规律直接写出⑤,⑥个方程及它们的解.
(2)请你用一个含正整数n的式子表示上述规律,并求出它的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点. 
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标. 注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(-2,2);C(2,-2).
为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(-2,2);C(2,-2).

(1) 请直接写出B点、C点、P点的对应点B1,C1,P1的坐标;
(2) 求△AOC的面积S△AOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
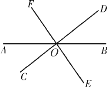
【题目】如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_________,∠AOC的邻补角是_______.若∠AOC=50°,则∠BOD=__________,∠COB=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
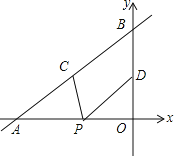
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com