
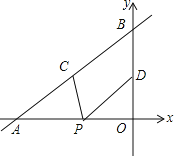
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
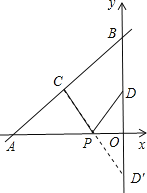
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=-6,
x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(-3,2),D′(0,-2),
∴有![]() ,解得:
,解得: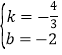 ,
,
∴直线CD′的解析式为y=-![]() x-2.
x-2.
令y=-![]() x-2中y=0,则0=-
x-2中y=0,则0=-![]() x-2,解得:x=-
x-2,解得:x=-![]() ,
,
∴点P的坐标为(-![]() ,0).
,0).
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
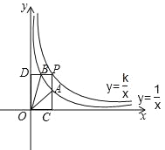
【题目】反比例函数![]() 和
和![]() (k≠0)在第一象限内的图象如图所示,点P在
(k≠0)在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥x轴,垂足为C,交
的图象上,PC⊥x轴,垂足为C,交![]() 的图象于点A,PD⊥y轴,垂足为D,交
的图象于点A,PD⊥y轴,垂足为D,交![]() 的图象于点B.已知点A(m,1)为线段PC的中点.
的图象于点B.已知点A(m,1)为线段PC的中点.
(1)求m和k的值;
(2)求四边形OAPB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角、同旁内角;
(3)指出FB,BC被AC所截形成的内错角、同旁内角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?
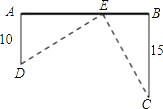
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角尺的直角顶点放在点O处
(1)如图①,若三角尺MON的一边ON与射线OB重合,则∠MOC= ;
(2)如图②,将三角尺MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数;
(3)将三角尺MON绕点O逆时针旋转至如图③所示的位置时,∠NOC=∠AOM,求∠NOB的度数.
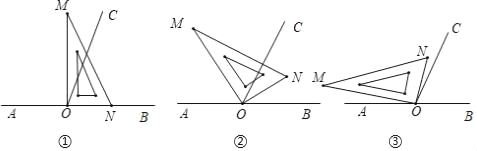
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
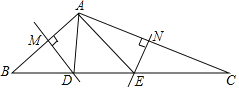
(1)若BC=8,则△ADE周长是多少?
(2)若∠BAC=118°,则∠DAE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司用10辆相同的汽车将一批苹果运到外地,每辆汽车能装8吨甲种苹果,或10吨乙种苹果,或11吨丙种苹果.公司规定每辆车只能装同一种苹果,而且必须满载.已知公司运送了甲、乙、丙三种苹果共100吨,且每种苹果不少于一车.
(1)设用x辆车装甲种苹果,y辆车装乙种苹果,求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若运送三种苹果所获利润的情况如下表所示:

设此次运输的利润为W(万元),问:如何安排车辆分配方案才能使运输利润W最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com