
����Ŀ��ij���乫˾��10����ͬ��������һ��ƻ���˵���أ�ÿ��������װ8�ּ���ƻ������10������ƻ������11�ֱ���ƻ������˾�涨ÿ����ֻ��װͬһ��ƻ�������ұ������أ���֪��˾�����˼ס��ҡ�������ƻ����100�֣���ÿ��ƻ��������һ����
��1������x����װ����ƻ����y����װ����ƻ������y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2������������ƻ�����������������±���ʾ��

��˴����������ΪW����Ԫ�����ʣ���ΰ��ų������䷽������ʹ��������W�������������
���𰸡���1��y��x֮��ĺ�����ϵʽΪ ![]() ���Ա���x��ȡֵ��Χ��x =1��x =2��x =3��
���Ա���x��ȡֵ��Χ��x =1��x =2��x =3��
��2����������������ķ���Ϊ����1����װ����ƻ������7����װ����ƻ����2����װ����ƻ����
�����������������
��1������������ƻ����������100t���г�����x��y�ķ������õ�y��x֮��ĺ�����ϵʽ��Ȼ����ÿ��ƻ��������һ������x��y�����������õ��Ա�����ȡֵ��Χ��
��2�����ݱ������������ݣ��õ�w��x֮��ĺ�����ϵʽ�����ɺ���������������Ա�����ȡֵ��Χ�������.
���������
��1����![]() ��
��
�� y��x֮��ĺ�����ϵʽΪ ![]() ��
��
�� y��1�����x��3��
�� x��1�� ![]() ��1����x����������
��1����x����������
�� �Ա���x��ȡֵ��Χ��x =1��x =2��x =3��
��2��![]() ��
��
��ΪW��x���������С������xȡ1ʱ���ɻ���������
��ʱ![]() ����Ԫ����
����Ԫ����
��������������ķ���Ϊ����1����װ����ƻ������7����װ����ƻ����2����װ����ƻ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC��BE��CE��E��AD��CE��D�� 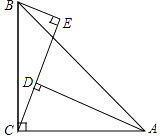
��1����֤����ADC�ա�CEB��
��2��AD=5cm��DE=3cm����BE�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BA=BC����ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E��BC���ӳ����ڡ�O������AF���ڵ�F��
��1����֤����ABC=2��CAF��
��2����AC=2![]() ��CE��EB=1��4����CE�ij���
��CE��EB=1��4����CE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���Լ������ѳ�Ϊ���dz��ε���Ҫ��ʽ����ʮһ������ڣ�ij��ʦ�ݽγ�����ɽ�������ϸ��ٹ�·;����ɽ�纣���źͺ�����纣���ŵ������¸��٣��������4.5Сʱ������ʱƽ���ٶ������10ǧ�ף�Сʱ����ȥʱ�����˰�Сʱ�ص���ɽ��
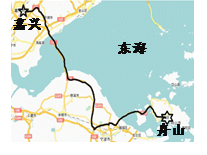
��1������ɽ��������ؼ�ĸ��ٹ�··�̣�
��2�������纣���ŵij��ȼ����ŷѼ��±���
�������� | ��ɽ�纣���� | ������纣���� |
���ų��� | 48ǧ�� | 36ǧ�� |
���ŷ� | 100Ԫ | 80Ԫ |
��ͨ���Ź涨���γ��ĸ��ٹ�·ͨ�з�![]() ��Ԫ���ļ��㷽��Ϊ��
��Ԫ���ļ��㷽��Ϊ�� ![]() ������
������![]() ��Ԫ��ǧ�ף�Ϊ���ٹ�·��̷ѣ�
��Ԫ��ǧ�ף�Ϊ���ٹ�·��̷ѣ� ![]() ��ǧ�ף�Ϊ���ٹ�·��̣��������纣���ų�����
��ǧ�ף�Ϊ���ٹ�·��̣��������纣���ų�����![]() ��Ԫ��Ϊ�纣���Ź��ŷѣ�������ʦ����ɽ�����������ĸ��ٹ�·ͨ�з�Ϊ295.4Ԫ����γ��ĸ��ٹ�·��̷�
��Ԫ��Ϊ�纣���Ź��ŷѣ�������ʦ����ɽ�����������ĸ��ٹ�·ͨ�з�Ϊ295.4Ԫ����γ��ĸ��ٹ�·��̷�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x2��3x��0��Ϊ��������
A.x��0B.x��3C.x��0��x��3D.x��0��x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ŀ�������ָ���ֱ���28��45��28��45��28��30��53���������ݵ�������(����)
A. 28 B. 30 C. 45 D. 53
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���찲���̳������ġ����硱�����̺��װ����С���ȵ�20֧���̣����̺еĶ��Ǻ�ʮ֧�������г����У���������һ֧���̵�ֱ��ԼΪ0.75cm����ԼΪ8.4cm�� 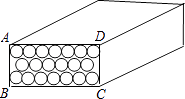
��1���Լ����̺ж���ABCD���������С���������ȡ����ֵ����
��2����������һ���̺�������Ҫ���������ֽ�ţ������ص�ճ�ϵIJ��֣���������ȷ��0.1cm�� ![]() ȡ1.73����
ȡ1.73����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ�ӹ����ƻ��ӹ�400���˶������ڼӹ���160�������¼���������Ч�ʱ�ԭ�ƻ������20%�����������18�����ȫ��������ԭ�ƻ�ÿ��ӹ��������˶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ������1��1��2��3��5��8��13���������дӵ���������ÿһ������������ǰ���������ĺͣ������������еĸ�������Ϊ�����εı߳�������ͼ1�����Σ��ٷֱ����δ�����ȡ2����3����4����5��������ƴ����ͼ2��ʾ�ij����β���Ϊ�������������ܣ������˹��ɼ����������Σ������Ϊ��ij����ε��ܳ���______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com