
【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,把△ABC沿对角线AC折叠,得到△AB'C,B'C与AD相交于点E,则AE的长 . 
【答案】5cm
【解析】解:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=8cm,CD=AB=4cm,
∴∠ACB=∠DAC.
由折叠的性质得:∠ACB=∠ECA,
∴∠DAC=∠ECA.
∴AE=CE,
设AE=x,则CE=x,DE=8﹣x,
在Rt△CDE中,DE2+CD2=CE2.
即(8﹣x)2+42=x2,
解得:x=5.
即AE=5,
所以答案是:5cm.
【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 如图1,线段AN与线段BM是否相等?证明你的结论;
(2) 如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 当路程一定时,时间与速度成正比例
B. “全等三角形的面积相等”的逆命题是真命题
C. ![]() 是最简二次根式
是最简二次根式
D. 到直线AB的距离等于1厘米的点的轨迹是平行于直线AB且和AB距离为1cm的一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2015次后,得到的等腰直角三角形的直角顶点P2016的坐标为( )
A.(4033,﹣1)
B.(4031,﹣1)
C.(4033,1)
D.(4031,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
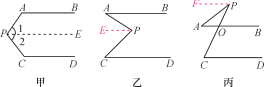
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),与y轴相交于点C,动点M在线段OA和射线AC上运动.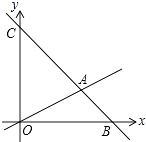
(1)求直线AB的解析式;
(2)若△OMC的面积是△OAC的面积的 ![]() ,请直接写出此时点M的坐标 .
,请直接写出此时点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
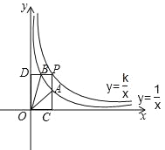
【题目】反比例函数![]() 和
和![]() (k≠0)在第一象限内的图象如图所示,点P在
(k≠0)在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥x轴,垂足为C,交
的图象上,PC⊥x轴,垂足为C,交![]() 的图象于点A,PD⊥y轴,垂足为D,交
的图象于点A,PD⊥y轴,垂足为D,交![]() 的图象于点B.已知点A(m,1)为线段PC的中点.
的图象于点B.已知点A(m,1)为线段PC的中点.
(1)求m和k的值;
(2)求四边形OAPB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
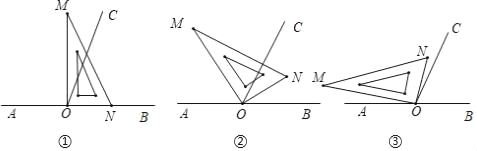
【题目】已知O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角尺的直角顶点放在点O处
(1)如图①,若三角尺MON的一边ON与射线OB重合,则∠MOC= ;
(2)如图②,将三角尺MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数;
(3)将三角尺MON绕点O逆时针旋转至如图③所示的位置时,∠NOC=∠AOM,求∠NOB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com