
【题目】图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 如图1,线段AN与线段BM是否相等?证明你的结论;
(2) 如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.

图1 图2
【答案】(1)相等,证明见解析;(2)△CEF的形状是等边三角形.
【解析】
(1)等边三角形的性质可以得出△ACN、△MCB两边及夹角分别对应相等,;两个三角形全等,得出线段AN=BM;(2)平角的定义得出∠MCN=60°,通过证明△ACE≌△MCF,得出CE=CF,根据等边三角形的判定得出△CEF的形状.
(1)∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°.
∴∠MCN=60°,∠ACN=∠MCB,
在△ACN和△MCB中,
AC=MC, ∠ACN=∠MCB,CN=CB,
∴△ACN≌△MCB(SAS),∴AN=BM.
(2)∵∠ACM=60°,∠MCN=60°,∴∠ACM=∠MCN,
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
在△ACE和△MCF中,
∠CAE=∠CMF,AC=MC, ∠ACE=∠MCF,
∴△ACE≌△MCF(ASA),
∴CE=CF,
∴△CEF的形状是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.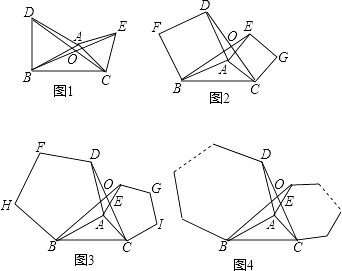
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数; 
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数; 
(3)在图3中,画一个正方形,使它的面积是10. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去新华书店,如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图象 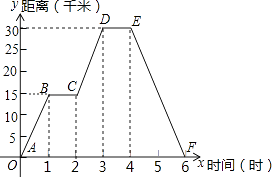
(1)根据图象回答:小明家离新华书店千米,小明用了小时到达新华书店;
(2)小明从家出发两个半小时走了千米;
(3)直线CD的函数解析式为;
(4)小明出发小时,离家12千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育局为了解七年级学生一个学期参加综合实践活动的情况,随机抽样调查了某校七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图),请你根据图中提供的信息,回答下列问题:
(1)求出该校七年级学生总数;
(2)在这次抽样调查中,众数和中位数分别是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC的三边长a,b,c满足(a-b)2+|b-2|+(c2-8)2=0,则下列对此三角形的形状描述最确切的是( )
A. 等边三角形 B. 等腰三角形 C. 等腰直角三角形 D. 直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河边有A,B两个村庄,A村距河边10 m,B村距河边30 m,两村平行于河边方向的水平距离为30 m,现要在河边建一抽水站,需铺设管道抽水到A村和B村.
(1)求铺设管道的最短长度是多少,请画图说明;
(2)若铺设管道每米需要500元,则最低费用为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com