
【题目】如图,河边有A,B两个村庄,A村距河边10 m,B村距河边30 m,两村平行于河边方向的水平距离为30 m,现要在河边建一抽水站,需铺设管道抽水到A村和B村.
(1)求铺设管道的最短长度是多少,请画图说明;
(2)若铺设管道每米需要500元,则最低费用为多少?

【答案】(1)铺设管道的最短长度是50m;(2)最低费用为25000元.
【解析】
(1)根据轴对称性质,过点A作AC⊥CE于点C,延长AC至点D,使CD=AC,
连接BD,交河边于点E,连接AE,则抽水站应建在点E处,可使铺设的管道最短,最短长度为AE+BE,即BD的长.过点B作BF⊥AC于点F,由题意得:AC=10 m,CF=30 m,BF=30 m,
CD=AC=10 m,DF=10+30=40(m),在Rt△BDF中,根据勾股定理可得:BD2=302+402=502,计算可得:BD=50(m),
(2)将最短距离乘以铺管道每米的单价可进行计算,最低费用为50×500=25000(元).
如图,过点A作AC⊥CE于点C,延长AC至点D,使CD=AC,
连接BD,交河边于点E,
连接AE,则抽水站应建在点E处,可使铺设的管道最短,最短长度为AE+BE,即BD的长.
过点B作BF⊥AC于点F,

由题意得:AC=10 m,CF=30 m,BF=30 m,
所以CD=AC=10 m,
所以DF=10+30=40(m),
在Rt△BDF中,BD2=302+402=502,
所以BD=50(m),
即铺设管道的最短长度是50 m.
(2)最低费用为50×500=25000(元).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣ ![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 如图1,线段AN与线段BM是否相等?证明你的结论;
(2) 如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( )
A.13
B.19
C.25
D.169
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与直线y= ![]() x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, ![]() ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.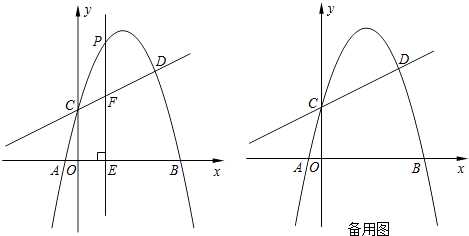
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com