
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数; 
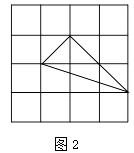
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数; 
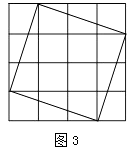
(3)在图3中,画一个正方形,使它的面积是10. 
【答案】
(1)解:三边分别为:3、4、5 (如图1)

(2)解:三边分别为: ![]() 、2
、2 ![]() 、
、 ![]() (如图2)
(如图2)
(3)解:画一个边长为 ![]() 的正方形(如图3)
的正方形(如图3)
【解析】(1)利用勾股定理,找长为有理数的线段,画三角形即可.(2)画一个边长 ![]() ,2
,2 ![]() ,
, ![]() 的三角形即可;(3)画一个边长为
的三角形即可;(3)画一个边长为 ![]() 的正方形即可.
的正方形即可.
【考点精析】解答此题的关键在于理解无理数的相关知识,掌握在理解无理数时,要抓住“无限不循环”这个要点,归纳起来有四类:(1)开方开不尽的数;(2)有特定意义的数,如圆周率π,或化简后含有π的数;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o等,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD的外接圆上的一动点(点C不在 ![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°
上,且不与点B,D重合),∠ACB=∠ABD=45° 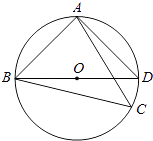
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证: ![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2 , AM2 , BM2三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=(用α表示);如图②,∠CBO= ![]() ∠ABC,∠BCO=
∠ABC,∠BCO= ![]() ∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
(2)如图③,∠CBO= ![]() ∠DBC,∠BCO=
∠DBC,∠BCO= ![]() ∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO= ![]() ∠DBC,∠BCO=
∠DBC,∠BCO= ![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣ ![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD,BC相交于点O,OA=OD,OB=OC.下列结论正确的是( )

A. △AOB≌△DOC B. △ABO≌△DOC C. ∠A=∠C D. ∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
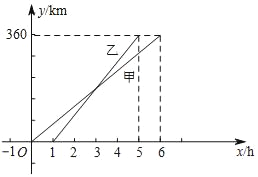
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑“之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米
②兔子和乌龟同时从起点出发
③乌龟在途中休息了10分钟
④兔子在途中750米处追上乌龟
其中说法正确的是( )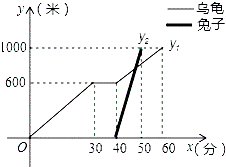
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 如图1,线段AN与线段BM是否相等?证明你的结论;
(2) 如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com