
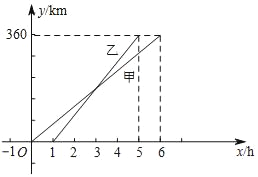
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?
【答案】(1)60.(2)y乙=90x﹣90;y甲=60x.()220km
【解析】
(1)根据图象确定出甲的路程与时间,即可求出速度;
(2)利用待定系数法即可解决问题;
(3)求出乙距A地240km时的时间,加上1,再乘以甲的速度即可得到结果.
(1)根据图象得:360÷6=60km/h.
故答案为:60.
(2)当1≤x≤5时,设y乙=kx+b,把(1,0)与(5,360)代入得: ,解得:k=90,b=﹣90,则y乙=90x﹣90;
,解得:k=90,b=﹣90,则y乙=90x﹣90;
当0<x≤6时,设y甲=mx,把(6,360)代入得到m=60,∴y甲=60x.
(3)∵乙与A地相距240km,且乙的速度为360÷(5﹣1)=90km/h,∴乙用的时间是240÷90= h,则甲与A地相距60×(
h,则甲与A地相距60×( +1)=220km.
+1)=220km.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】 甲、乙两名车工都加工要求尺寸是直径10毫米的零件.从他们所生产的零件中,各取5件,测得直径如下(单位:毫米)
甲:10.05, 10.02,9.97,9.95,10.01
乙:9.99,10.02,10.02,9.98,10.01
分别计算两组数据的标准差(精确到0.01),说明在尺寸符合规格方面,谁做得较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.

(探究思考)
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.

(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数; 
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数; 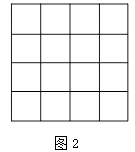
(3)在图3中,画一个正方形,使它的面积是10. 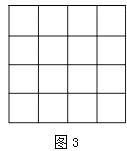
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B;直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q.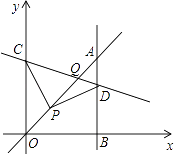
(1)求证:OB=OC;
(2)当点C坐标为(0,3)时,求点Q的坐标;
(3)当△OPC≌△ADP时,直接写出C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育局为了解七年级学生一个学期参加综合实践活动的情况,随机抽样调查了某校七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图),请你根据图中提供的信息,回答下列问题:
(1)求出该校七年级学生总数;
(2)在这次抽样调查中,众数和中位数分别是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某中学八年级的1000名学生最喜欢的球类活动统计表:
最喜欢的 球类活动 | 篮球 | 排球 | 足球 | 乒乓球 | 其他 |
人数 | 185 | 175 | 260 | 330 | 50 |
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎的程度差不多?
(3)八年级学生最喜欢的各类球类活动的频率各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com