
【题目】(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.

(探究思考)
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.

(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.

【答案】EF=BE+DF
【解析】
问题1,先证明△CBE≌△CDG,再证明△CEF≌△CGF,最后用线段的和差即可得出结论;
问题2、先判断出∠ABC=∠GDC,进而判断出△CBE≌△CDG,再证明△CEF≌△CGF,最后用线段的和差即可得出结论;
问题3、同问题2的方法即可得出结论.
问题1、BE+FD=EF,
理由:延长FD到点G.使DG=BE.连结CG,
在△CBE和△CDG中,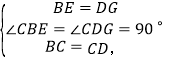
∴△CBE≌△CDG(SAS),
∴CE=CG,∠BCE=∠DCG,
∵![]()
∴![]()
∵![]()
∴∠ECF=∠GCF,
在△CEF和△CGF中,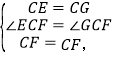
∴△CEF≌△CGF,
∴EF=GF,
∴EF=DF+DG=DF+BE;
故答案为:EF=DF+BE;
问题2,问题1中结论仍然成立,如图2,
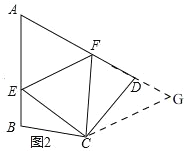
理由:延长FD到点G.使DG=BE.连结CG,
∵![]()
∴∠ABC=∠GDC,
在△CBE和△CDG中,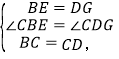
∴△CBE≌△CDG(SAS),
∴CE=CG,∠BCE=∠DCG,
∴∠BCD=∠ECG,
∵![]()
∴![]()
∴∠ECF=∠GCF,
在△CEF和△CGF中,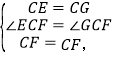
∴△CEF≌△CGF,
∴EF=GF,
∴EF=DF+DG=DF+BE;
问题3.结论:DF=EF+BE;理由:如图3,
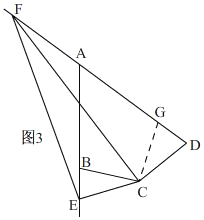
延长FD到点G.使DG=BE.连结CG,
∵![]()
∴∠ABC=∠GDC
在△CBE和△CDG中,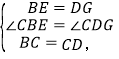
∴△CBE≌△CDG(SAS),
∴CE=CG,∠BCE=∠DCG,
∴∠BCD=∠ECG,
∵![]()
∴![]()
∴∠ECF=∠GCF,
在△CEF和△CGF中, 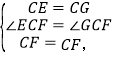
∴△CEF≌△CGF,
∴EF=GF,
∴DF=FG+DG=EF+BE;


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30 ![]() m到达A′处,
m到达A′处,
(1)求A,B之间的距离;
(2)求从无人机A′上看目标D的俯角的正切值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
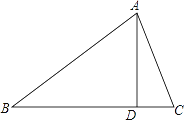
【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16
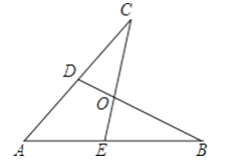
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣ ![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 . 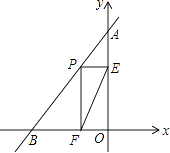
查看答案和解析>>
科目:初中数学 来源: 题型:
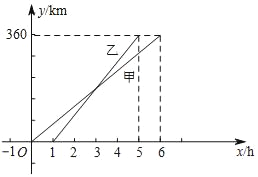
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD. 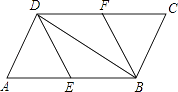
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( )
A.13
B.19
C.25
D.169
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com