
【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
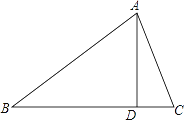
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16
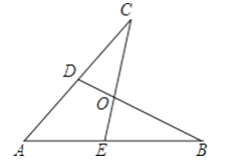
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
科目:初中数学 来源: 题型:
【题目】某中学数学活动小组为了调查居民的用水情况,从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
月用水量(吨) | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
户 数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
(1)求这30户家庭月用水量的平均数,众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为m(吨),家庭月用水量不超过m(吨)的部分按原价收费,超过m吨部分加倍收费,你认为上述问题中的平均数、众数、中位数中哪一个量作为月基本用水量比较合理?简述理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径 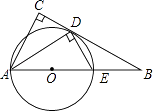
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.

(探究思考)
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.

(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B;直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q.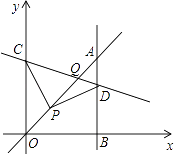
(1)求证:OB=OC;
(2)当点C坐标为(0,3)时,求点Q的坐标;
(3)当△OPC≌△ADP时,直接写出C点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com