
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B;直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q.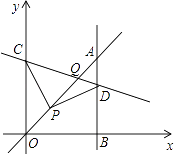
(1)求证:OB=OC;
(2)当点C坐标为(0,3)时,求点Q的坐标;
(3)当△OPC≌△ADP时,直接写出C点的坐标.
【答案】
(1)
证明:过P作GH⊥OC,垂足为G,交AB于H,
过P作PE⊥x轴,垂足为E,
∵AB⊥OB,
∴GH⊥AB,
∵∠CPD=90°,
∴∠GPC+∠DPH=90°,
∠GCP+∠GPC=90°,
∴∠GCP=∠DPH,
又∵∠CGP=∠PHD=90°,PC=PD,
∴△CGP≌△PHD,
∴CG=PH,
∵∠PEB=∠EBH=∠BHP=90°,
∴四边形PEBH为矩形,
∴PH=EB,
∴CG=EB,
∵GH∥OB,OG∥PE,∠GOE=90°,
∴四边形GOEP为矩形,
∵直线OA:y=x,
∴∠GOP=∠POE=45°,
∵∠GPO=∠POE=45°,
∴∠GOP=∠GPO,
∴GO=GP,
∴矩形GOEP为正方形,
∴OG=OE,
∴OG+GC=OE+EB,
即OC=OB
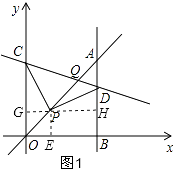
(2)
证明:∵P(1,1),
∴OG=BH=PG=DH=1,
∵C(0,3),
∴OB=OC=3,
∴D(3,2),
设直线CD的解析式为:y=kx+b,
把D(3,2)、C(0,3)代入得: ![]() ,
,
解得 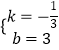 ,
,
∴直线CD的解析式为:y=﹣ ![]() x+3,
x+3,
则 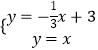 解得
解得 ![]() ,
,
∴Q( ![]() ,
, ![]() )
)
(3)
证明:如图2,过P作GH⊥OC,垂足为G,交AB于H,
设CG=x,则PH=x,OC=x+1,
∵△OPC≌△ADP,
∴AP=OC=x+1,AD=OP= ![]() ,
,
∴AH= ![]() +1,
+1,
在Rt△APH中,由勾股定理得:(x+1)2=x2+( ![]() +1)2,
+1)2,
x= ![]() +1,
+1,
∴C(0,2+ ![]() ).
).
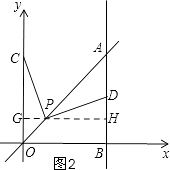
【解析】(1)作辅助线,构建全等三角形,证明CG=EB,证明四边形OGPE为正方形得OG=OE,所以OC=OB;(2)先求点D的坐标,再利用待定系数法求直线CD的解析式,与直线OA的解析式列方程组求出点Q的坐标;(3)设CG=x,根据△OPC≌△ADP表示出直角三角形APH各边的长,利用勾股定理列方程求出x的值,写出点C的坐标.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等,![]() =
=![]() =
=![]() ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵![]() =
=![]() ∴b=
∴b=![]() =
=![]() =
=![]() =3
=3![]() .
.
理解应用:
如图,甲船以每小时30![]() 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里.
海里.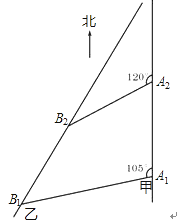
(1)判断△A1A2B2的形状,并给出证明
(2)求乙船每小时航行多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
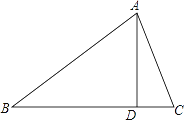
【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16
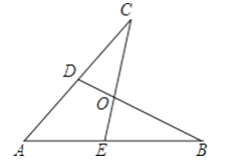
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 . 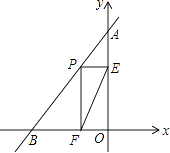
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?
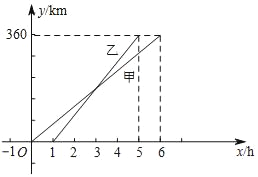
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
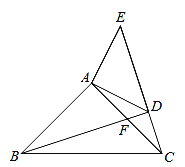
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD. 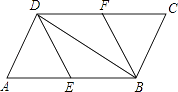
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;②△ABC的三边长分别为a,b,c,若a2+b2=c2,则∠A=90°;③在△ABC中,若∠A∶∠B∶∠C=1∶5∶6,则△ABC是直角三角形;④若三角形的三边长之比为3∶4∶5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com