
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD. 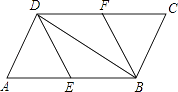
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
【答案】
(1)证明:在平行四边形ABCD中,∠A=∠C,AD=BC,
∵E、F分别为AB、CD的中点,
∴AE=CF.
在△ADE和△CBF中, 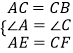
∴△ADE≌△CBF(SAS)
(2)解:若AD⊥BD,则四边形BFDE是菱形.
证明:∵AD⊥BD,
∴△ABD是直角三角形,且∠ADB=90°.
∵E是AB的中点,
∴DE= ![]() AB=BE.
AB=BE.
∵在ABCD中,E,F分别为边AB,CD的中点,
∴EB∥DF且EB=DF,
∴四边形BFDE是平行四边形.
∴四边形BFDE是菱形
【解析】(1)根据题中已知条件不难得出,AD=BC,∠A=∠C,E、F分别为边AB、CD的中点,那么AE=CF,这样就具备了全等三角形判定中的SAS,由此可得出△AED≌△CFB.(2)直角三角形ADB中,DE是斜边上的中线,因此DE=BE,又由DE=BF,FD∥BE那么可得出四边形BFDE是个菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.

(探究思考)
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.

(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B;直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q.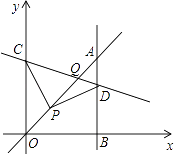
(1)求证:OB=OC;
(2)当点C坐标为(0,3)时,求点Q的坐标;
(3)当△OPC≌△ADP时,直接写出C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育局为了解七年级学生一个学期参加综合实践活动的情况,随机抽样调查了某校七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图),请你根据图中提供的信息,回答下列问题:
(1)求出该校七年级学生总数;
(2)在这次抽样调查中,众数和中位数分别是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新世纪广场进货员预测一种应季衬衫能畅销市场,就用8万元购进这种衬衫,面市后果然供不应求,商场又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了4元,商场销售这种衬衫时每件定价都是58元,最后剩下的150件按八折销售,很快售完,在这两笔生意中,商场共赢利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com