
【题目】(8分)将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形.

【答案】(1)∠1=52°;(2)证明见解析.
【解析】
试题(1)图形的折叠中隐含着角和线段的相等,由题, 将一张矩形纸条ABCD按如图所示沿EF折叠,∠FEC=64o, ∠FEC′=64o,即∠BEC′=180o-∠FEC-∠FEC′= 52o,因为AD∥BC,所以∠1=∠AGC′=∠BEC′=52o;
(2)只要找到两个底角相等即可,因为∠FEC=64o,AD∥BC,所以∠GFE=∠FEC=64o,又因为∠FEC′=64o,所以GF=GE, 即△EFG是等腰三角形.
试题解析:(1)如图:∵∠FEC=64o,据题意可得:∠FEC′=64o,
∴∠BEC′=180o-∠FEC-∠FEC′= 52o,
又∵AD∥BC,
∴∠1="∠AGC′=" ∠BEC′=52o.
(2)证明:∵∠FEC=64o,AD∥BC,
∴∠GFE=∠FEC=64o,
又∵∠FEC′=64o,
∴∠FEG=∠GEF=64o,
∴GF=GE,即△EFG是等腰三角形.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.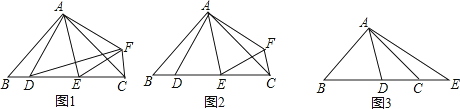
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 . 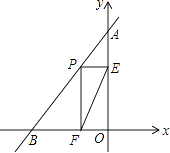
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
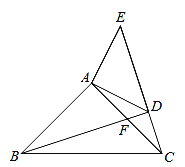
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD. 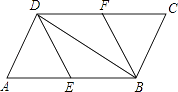
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)已知:如图1,在正方形ABCD中,点E、H分别在BC、AB上,若AE⊥DH于点O,求证AE=DH;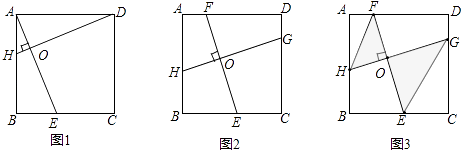
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
拓展应用:
(3)已知,如图3,在(2)问条件下,若BC=4,E为BC的中点,AF= ![]() AD,求HG的长
AD,求HG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;②△ABC的三边长分别为a,b,c,若a2+b2=c2,则∠A=90°;③在△ABC中,若∠A∶∠B∶∠C=1∶5∶6,则△ABC是直角三角形;④若三角形的三边长之比为3∶4∶5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定: ![]() (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如: ![]() ,已知T(1,﹣1)=﹣2,T(4,2)=1
,已知T(1,﹣1)=﹣2,T(4,2)=1
(1)求a,b的值;
(2)若关于m的不等式组 ![]() 恰好有4个整数解,求实数p的取值范围.
恰好有4个整数解,求实数p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com