
【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
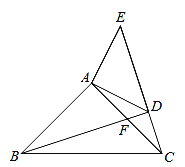
【答案】BD=CE,BD⊥CE;证明见解析.
【解析】
试题分析:根据全等三角形的判定得出△BAD≌△CAE,进而得出∠ABD=∠ACE,求出∠DBC+∠DCB=∠DBC+∠ACE+∠ACB即可得出答案.
试题解析:BD=CE,BD⊥CE;
理由:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD和△CAE中,
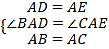 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.


科目:初中数学 来源: 题型:
【题目】对于二次函数y=﹣ ![]() +x﹣4,下列说法正确的是( )
+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本,一般在甲、乙两家文具店购买,已知两家文具店的标价都是每本1元,但甲文具店的优惠条件是一次购买10本以上,从第11本起按标价的70%卖;乙文具店的优惠条件是全部按八五折优惠.
(1)若小明打算买30本,到哪家店购买省钱?
(2)小明现有38元钱,最多可买多少本练习本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4 ![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F 
(1)求证: ![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过 点A,C 画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )

A. SSS B. SAS C. ASA D. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( ) 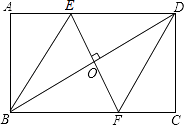
A.2 ![]()
B.3 ![]()
C.![]()
![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.(1)△ABF与△DCE全等吗?请说明理由;(2)AB与CD平行吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=1,连接AC,以AC为边作第一个正方形ACC1D1 , 连接AC1 , 以AC1为边作第二个正方形AC1C2D2 , 则第10个正方形边长为( ) 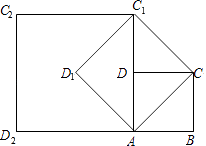
A.8
B.16
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图1),图2是侧面示意图.已知自动扶梯AC的坡度为i=1:2.4,AC=13m,BE是二楼楼顶,EF∥MN,B是EF上处在自动扶梯顶端C正上方的一点,且BC⊥EF,在自动扶梯底端A处测得B点仰角为42°.(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90) 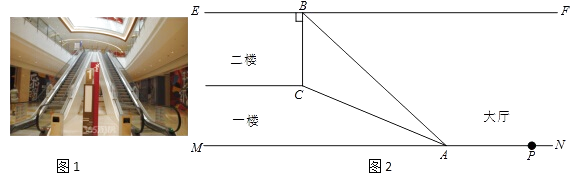
为了吸引顾客,开发商想在P处放置一个高10m的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出2m距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com