
【题目】对于二次函数y=﹣ ![]() +x﹣4,下列说法正确的是( )
+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣ ![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.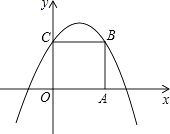
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.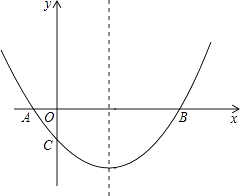
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y= ![]() (x>0)相交于点P(1,m ).
(x>0)相交于点P(1,m ).
(1)求k的值;
(2)若点Q与点P关于直线y=x成轴对称,则点Q的坐标是Q();
(3)若过P、Q二点的抛物线与y轴的交点为N(0, ![]() ),求该抛物线的函数解析式,并求出抛物线的对称轴方程.
),求该抛物线的函数解析式,并求出抛物线的对称轴方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG. 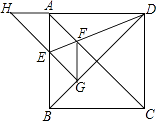
则下列结论:
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B
(1)求m的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;
(3)当 ![]() <m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.
<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
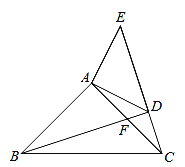
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com