
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.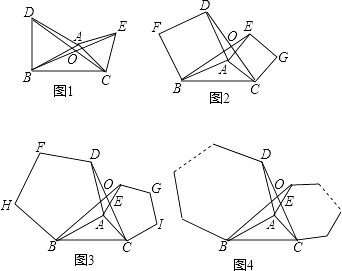
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
【答案】
(1)
证明:如图1,∵△ABD和△ACE是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
∴△ABE≌△ADC

(2)
证明:如图2,∠BOC=90°,理由是:
∵四边形ABFD和四边形ACGE都是正方形,
∴AB=AD,AC=AE,∠DAB=∠EAC=90°,
∴∠BAE=∠DAC,
∴△ADC≌△ABE,
∴∠BEA=∠DCA,
∵∠EAC=90°,
∴∠AMC+∠DCA=90°,
∵∠BOC=∠OME+∠BEA=∠AMC+∠DCA,
∴∠BOC=90°
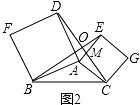
(3)72°
(4)![]()
【解析】证明:(3)如图3,同理得:△ADC≌△ABE,
∴∠BEM=∠DCA,
∵∠BOC=∠BEM+∠OME=∠DCA+∠AMC,
∵正五边形ACIGE,
∴∠EAC=180°﹣ ![]() =108°,
=108°,
∴∠DCA+∠AMC=72°,
∴∠BOC=72°;
故答案为:72°;
4)如图4,∠BOC的度数为 ![]() ,理由是:
,理由是:
同理得:△ADC≌△ABE,
∴∠BEA=∠DCA,
∵∠BOC=∠BEA+∠OME=∠DCA+∠AMC,
∵正n边形AC…E,
∴∠EAC=180°﹣ ![]() ,
,
∴∠DCA+∠AMC=180°﹣(180﹣ ![]() )°,
)°,
∴∠BOC= ![]() .
.
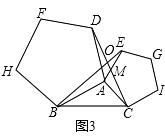
(1)根据等边三角形证明AB=AD,AC=AE,再利用等式性质得∠DAC=∠BAE,根据SAS得出△ABE≌△ADC;(2)根据正方形性质证明△ABE≌△ADC,得∠BEA=∠DCA,再由正方形ACEG的内角∠EAC=90°和三角形外角和定理得∠BOC=90°;(3)根据正五边形的性质证明:△ADC≌△ABE,再计算五边形每一个内角的度数为108°,由三角形外角定理求出∠BOC=72°;(4)根据正n边形的性质证明:△ADC≌△ABE,再计算n边形每一个内角的度数为180°﹣ ![]() ,由三角形外角定理求出∠BOC=
,由三角形外角定理求出∠BOC= ![]() .本题是四边形的综合题,考查了全等三角形、等边三角形、正四边形等图形的性质,关键是利用正n边形各边相等证明两三角形全等,运用了类比的方法,同时还要熟练掌握正n边形每一个内角的求法:可以利用外角和求,也可以利用内角和求;根据三角形的一个外角等于与它不相邻的两个内角和列式并综合对顶角相等分别得出结论.
.本题是四边形的综合题,考查了全等三角形、等边三角形、正四边形等图形的性质,关键是利用正n边形各边相等证明两三角形全等,运用了类比的方法,同时还要熟练掌握正n边形每一个内角的求法:可以利用外角和求,也可以利用内角和求;根据三角形的一个外角等于与它不相邻的两个内角和列式并综合对顶角相等分别得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:
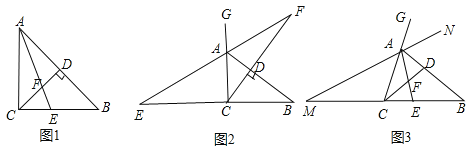
(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD的外接圆上的一动点(点C不在 ![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°
上,且不与点B,D重合),∠ACB=∠ABD=45° 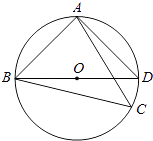
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证: ![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2 , AM2 , BM2三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试找出如图所示的每个正多边形的对称轴的条数,并填入表格中.
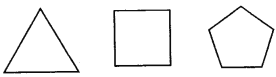
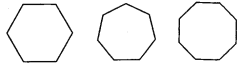
正多边形的边数 | 3 | 4 | 5 | 6 | 7 | 8 |
对称轴的条数 |
根据上表,请就一个正n边形对称轴的条数作一猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.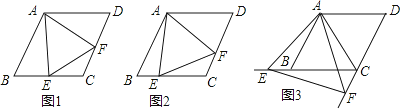
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=(用α表示);如图②,∠CBO= ![]() ∠ABC,∠BCO=
∠ABC,∠BCO= ![]() ∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
(2)如图③,∠CBO= ![]() ∠DBC,∠BCO=
∠DBC,∠BCO= ![]() ∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO= ![]() ∠DBC,∠BCO=
∠DBC,∠BCO= ![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣ ![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.
(1) 如图1,线段AN与线段BM是否相等?证明你的结论;
(2) 如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com